Quảng cáo
2 câu trả lời 12596
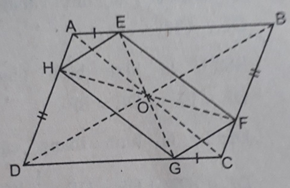
a, Xét ΔHAE và ΔFCG
Có : HAEˆ=FCGˆ ( 2 góc đối của hình bình hành )
AE = GC ( theo gt )
AH = FC ( Vì AD = BC mà AE = GC ,theo gt )
ΔHAE = ΔFCG ( c.g.c )
HE = GF ( 2 cạnh tương ứng ) [1]
Xét ΔHDG và ΔFBE
Có : HDGˆ=FBEˆ ( 2 góc đối của hình bình hành )
HD = BF
DG = BE ( Vì AB = DC mà HD = BF ,theo gt )
ΔHDG = ΔFBE ( c.g.c )
HG = EF ( 2 cạnh tương ứng ) [2]
Từ [1] và [2] EFGH là hình bình hành ( vì có các cạnh đối bằng nhau )
b, Có ABCD là hình bình hành AC cắt BD ở trung điểm mỗi đường [3]
Lại có EFGH cũng là hình bình hành EG cắt HF tại trung điểm mỗi đường[4]
Mà HBFD là hình bình hành ( vì HD // BF và HD = BF , theo gt )
HF cắt BD tại trung điểm mỗi đường [5]
Từ [3] ; [4] và [5] AC,BD,EG,FH đồng qui tại một điểm
Đ/s a, Tứ giác EFGH là hình bình hành
b) Các đường thẳng AC, BD , EG, FH đồng quy.
a, Xét ΔHAE và ΔFCG
Có : HAEˆ=FCGˆ ( 2 góc đối của hình bình hành )
AE = GC ( theo gt )
AH = FC ( Vì AD = BC mà AE = GC ,theo gt )
ΔHAE = ΔFCG ( c.g.c )
HE = GF ( 2 cạnh tương ứng ) [1]
Xét ΔHDG và ΔFBE
Có : HDGˆ=FBEˆ ( 2 góc đối của hình bình hành )
HD = BF
DG = BE ( Vì AB = DC mà HD = BF ,theo gt )
ΔHDG = ΔFBE ( c.g.c )
HG = EF ( 2 cạnh tương ứng ) [2]
Từ [1] và [2] EFGH là hình bình hành ( vì có các cạnh đối bằng nhau )
b, Có ABCD là hình bình hành AC cắt BD ở trung điểm mỗi đường [3]
Lại có EFGH cũng là hình bình hành EG cắt HF tại trung điểm mỗi đường[4]
Mà HBFD là hình bình hành ( vì HD // BF và HD = BF , theo gt )
HF cắt BD tại trung điểm mỗi đường [5]
Từ [3] ; [4] và [5] AC,BD,EG,FH đồng qui tại một điểm
Đ/s a, Tứ giác EFGH là hình bình hành
b) Các đường thẳng AC, BD , EG, FH đồng quy.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107437
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68061
Đã trả lời bởi chuyên gia
68061 -
 Đã trả lời bởi chuyên gia
52846
Đã trả lời bởi chuyên gia
52846 -
 Đã trả lời bởi chuyên gia
47344
Đã trả lời bởi chuyên gia
47344 -
 Đã trả lời bởi chuyên gia
45400
Đã trả lời bởi chuyên gia
45400 -
 Đã trả lời bởi chuyên gia
45045
Đã trả lời bởi chuyên gia
45045 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38412
Đã trả lời bởi chuyên gia
38412 -
 Đã trả lời bởi chuyên gia
38191
Đã trả lời bởi chuyên gia
38191


