Cho tam giác ABC vuông tại A có AB = 6cm, BC = 10cm.
a, Tính AC.
b, Trên tia đối của tia AB lấy điểm D sao cho A là trung điểm của BD. Chứng minh tam giác BCD cân.
c, Gọi K là trung điểm của BC, DK cắt AC tại M. Tính AM.
d, Đường trung trực của d của AC cắt DC tại Q. Chứng minh B, M, Q thẳng hàng.
Quảng cáo
2 câu trả lời 1346
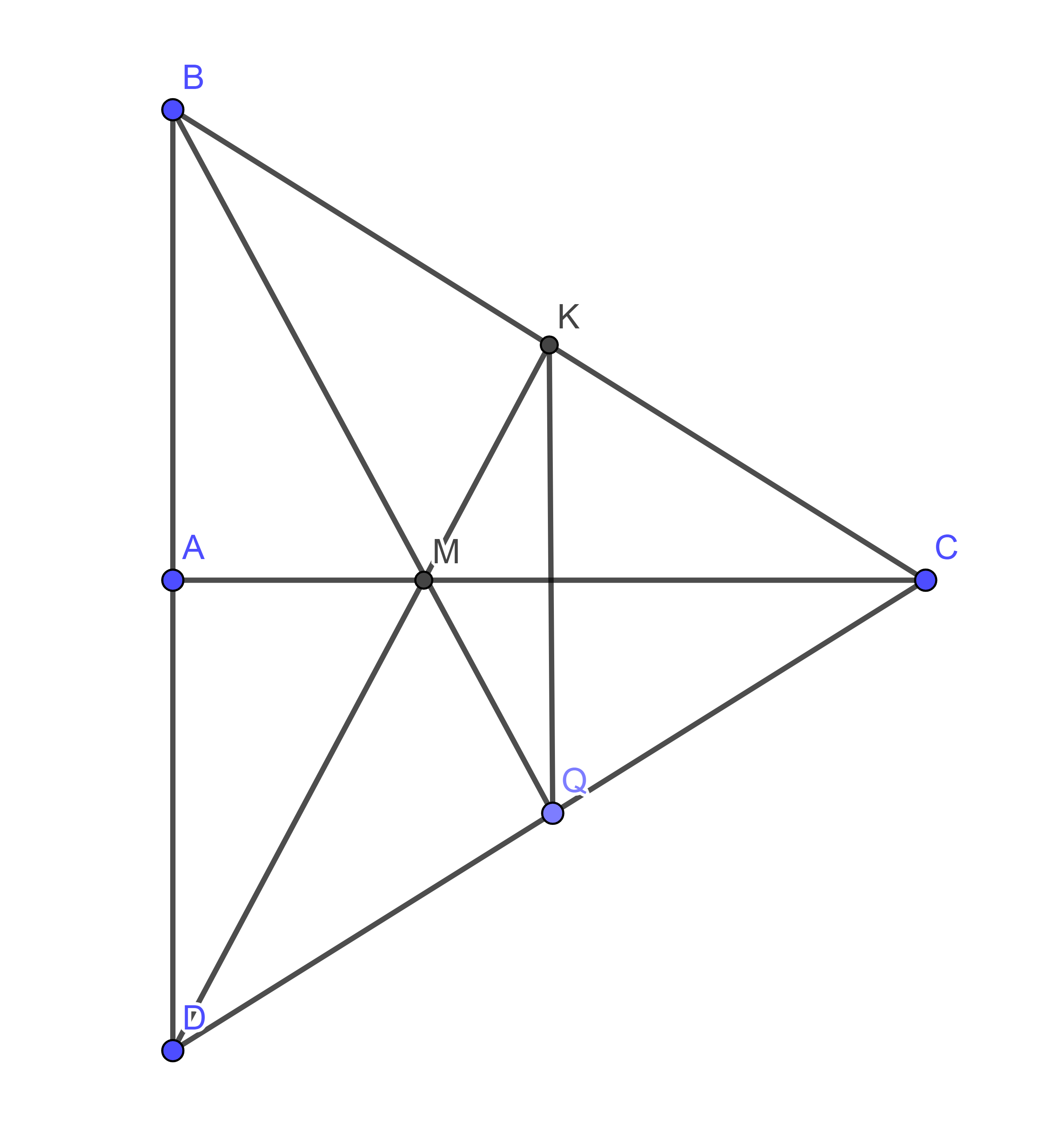
a) Xét tam giác BAC vuông tại A
Áp dụng Pytago ta có:
\(\begin{array}{l}
B{C^2} = A{B^2} + A{C^2}\\
= > AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{10}^2} - {6^2}} = 8(cm)
\end{array}\)
b) Xét tam giác ABC và tam giác ADC có:
AB=AD
Góc BAC=góc DAC=90
AC chung
=>Tam giác BAC=tam giác ADC(c-g-c)
=> BC=DC(2 cạnh tương ứng)
Xét tam giác BDC có: BC=DC
=>Tam giác BDC cân tại C
c)Xét tam giác BDC có DK và CA là 2 trung tuyến
DK cắt CA tại M
=>M là trọng tâm tam giác BCD
=> CM=2/3.CA
=> AM=1/3 AC=1/3. 8=8/3(cm)
d)
ta có Q thuộc trung trực của AC
=> QA=QC (tính chất đường trung trực)
=>tam giác QAC cân tại Q
=>Góc QAC=góc QCA
Có góc QAC+góc QAD=90
Góc QCA+góc ADQ=90
=>Góc QAD=góc ADQ
=>Tam giác QAD cân tại Q
=> QA=QD
=> QC=QD
=> Q là trung điểm của DC
Xét tam giác BDC có BQ là trung tuyến
M là trọng tâm tam giác
=> M thuộc BD hay B;M;Q thẳng hàng (đpcm)
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK121162
-
 Đã trả lời bởi chuyên gia
81971
Đã trả lời bởi chuyên gia
81971 -
 Đã trả lời bởi chuyên gia
59862
Đã trả lời bởi chuyên gia
59862 -
 Đã trả lời bởi chuyên gia
39757
Đã trả lời bởi chuyên gia
39757


