Cho 2 tam giác ABC và DBC chung cạnh huyền BC (A,D thuộc cùng một nửa mặt phẳng BC). Vẽ tia Ax sao cho AC là phân giác góc DAx. Vẽ tia Dy sao cho DB là phân giác góc ADy; Ax cắt Dy tại E, O là giao điểm Ac và BD
a) Chứng minh OE vuông góc BE
b) Chứng minh B,E,C thẳng hàng
Quảng cáo
1 câu trả lời 577
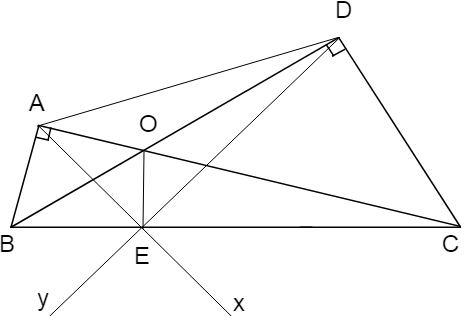
a) AC là phân giác của ^DAx (gt) mà ^BAC = 90 độ (gt) nên AB là phân giác ngoài tại đỉnh A của ΔADE
Kết hợp với DB là phân giác trong tại đỉnh D của ΔADE
=> BE là phân giác của ^AEy
Mà EO là phân giác của ^AED (3 đường phân giác trong của ΔAED đồng quy tại 1 điểm )
=> ^BEO = 90 độ (hai đường phân giác của hai góc kề bù)
Vậy OE ⊥BE (đpcm)
b) Chứng minh tương tự câu a, ta được OE⊥EC
Từ đó suy ra BE≡CE
Vậy B,E,C thẳng hàng (đpcm)
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120962
-
 Đã trả lời bởi chuyên gia
81713
Đã trả lời bởi chuyên gia
81713 -
 Đã trả lời bởi chuyên gia
59651
Đã trả lời bởi chuyên gia
59651 -
 Đã trả lời bởi chuyên gia
39669
Đã trả lời bởi chuyên gia
39669


