Quảng cáo
1 câu trả lời 409
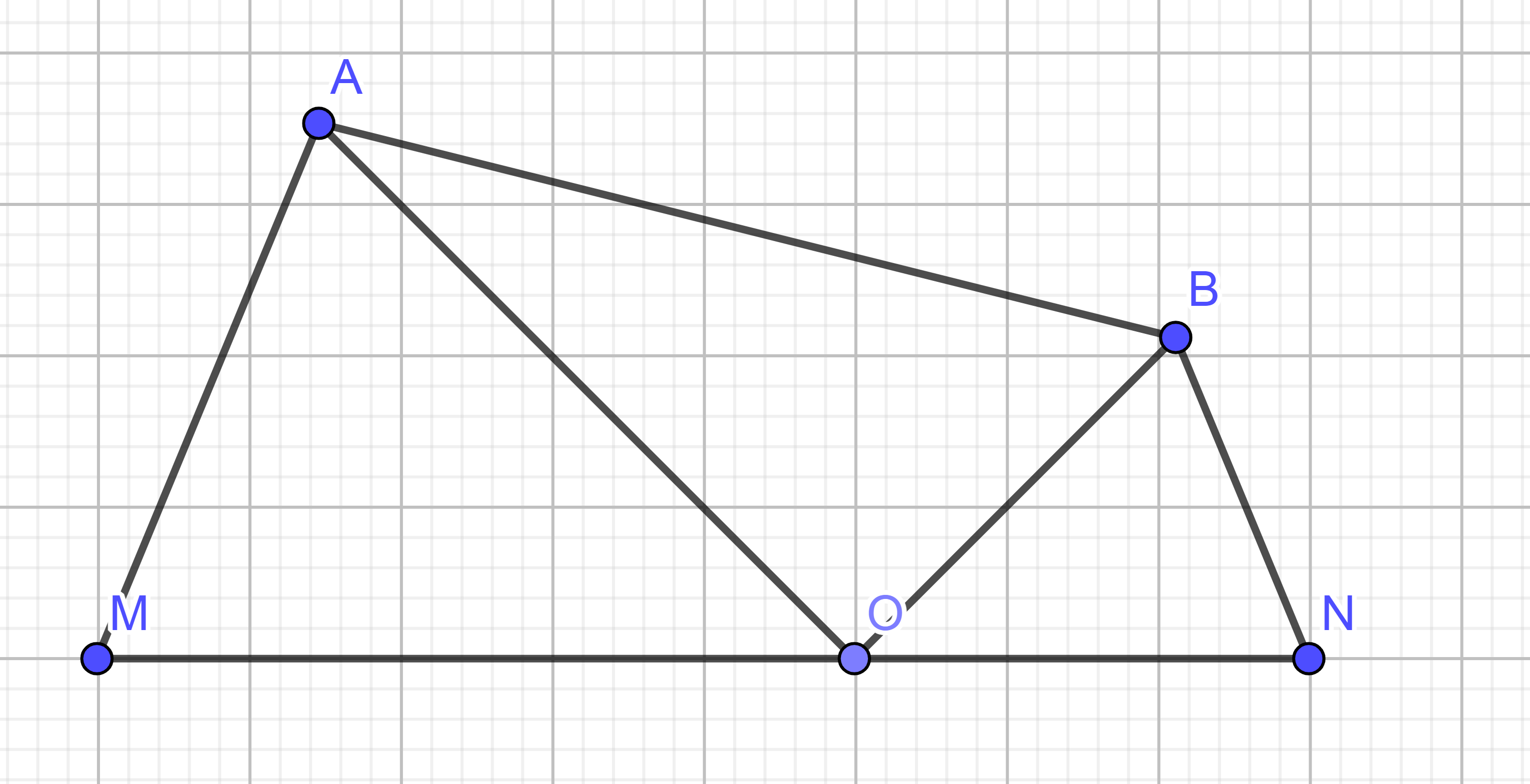
Ta có tam giác OAM và tam giác BON cân tại O có góc ở đỉnh O=45độ
=> OA=OM=a;OB=ON=b và góc MOA=góc NOB=45 độ
=>Góc AOB=180-45-45=90 độ
ta có OM+ON=MN=4
=>a+b=4
=>b=4-a
Xét tam giác AOB vuông tại O có:
Áp dụng định lý Pytago:
\(\begin{array}{l}
A{B^2} = A{O^2} + B{O^2} = {a^2} + {b^2}\\
= {a^2} + {(4 - a)^2}\\
= {a^2} + (16 - 8a + {a^2})\\
= {a^2} + {a^2} - 8a + 16\\
= 2{a^2} - 8a + 16\\
= 2({a^2} - 4a + 4) + 8\\
= 2{(a - 2)^2} + 8\\
De:A{B_{\min }} \Leftrightarrow A{B^2}_{\min } \Leftrightarrow 2{(a - 2)^2} + {8_{\min }}\\
Do:2{(a - 2)^2} \ge 0\\
= > 2{(a - 2)^2} + 8 \ge 8\forall a
\end{array}\)
Dấu = xảy ra<=> a-2=0<=>a=2
Hay OM=2(cm)
=>ON=4-2=2(cm)
=>O là trung điểm của MN
Vậy để ABmin=8 thì O là trung điêm của MN
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120761
-
81498
-
59515


