Quảng cáo
2 câu trả lời 20811
Bước 1: Xét điều kiện hệ số bậc cao của
Để hàm số y nghịch biến trên , đạo hàm của y, ký hiệu y', phải thỏa mãn:
![]()
Tính đạo hàm của y:
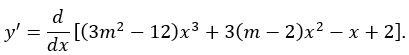
![]()
Điều kiện để hàm số nghịch biến trên là:
![]()
—
Bước 2: Xét hệ số a = 3m2 -12
Ta chia thành hai trường hợp:
Trường hợp 1: 3m2 -12 = 0
Giải phương trình:
![]()
- Với m = 2: Hàm số trở thành:
y = -x + 2
Đây là hàm số bậc nhất nghịch biến trên (thỏa mãn). - Với m = -2: Hàm số trở thành:
y = -12x3 - x + 2
Hệ số bậc cao -12 < 0, nên hàm số không nghịch biến trên toàn bộ (không thỏa mãn).
—
Trường hợp 2:
Khi đó y' là một hàm bậc hai có dạng:
![]()
Để ![]() , phương trình y' = 0 không có nghiệm, tức là hệ số
, phương trình y' = 0 không có nghiệm, tức là hệ số ![]() phải âm:
phải âm:
![]()
Giải bất phương trình:
![]()
Kết hợp với (m là số nguyên), ta có:
m = 0,1,-1
—
Bước 3: Tổng hợp các nghiệm thỏa mãn
Từ hai trường hợp trên, các giá trị của thỏa mãn là:
m = 0,1,2.
Bước 4: Tính tổng bình phương các giá trị của
Tổng bình phương các giá trị m là:
S = 02 + 12 + 22
Tính:
S = 0 + 1 + 4 = 5
—
Kết luận
Tổng bình phương các giá trị nguyên của m để hàm số nghịch biến trên là:
![]()
Bước 1: Xét điều kiện hệ số bậc cao của
Để hàm số y nghịch biến trên R, đạo hàm của y, ký hiệu y', phải thỏa mãn:
Tính đạo hàm của y:
Điều kiện để hàm số nghịch biến trên R là:
—
Bước 2: Xét hệ số a = 3m2 -12
Ta chia thành hai trường hợp:
Trường hợp 1: 3m2 -12 = 0
Giải phương trình:
Với m = 2: Hàm số trở thành:
y = -x + 2
Đây là hàm số bậc nhất nghịch biến trên R (thỏa mãn).
Với m = -2: Hàm số trở thành:
y = -12x3 - x + 2
Hệ số bậc cao -12 < 0, nên hàm số không nghịch biến trên toàn bộ R (không thỏa mãn).
—
Trường hợp 2: 3m2 − 12 ≠ 0
Khi đó y' là một hàm bậc hai có dạng:
Để , phương trình y' = 0 không có nghiệm, tức là hệ số phải âm:
Giải bất phương trình:
Kết hợp với m ∈ Z (m là số nguyên), ta có:
m = 0,1,-1
—
Bước 3: Tổng hợp các nghiệm thỏa mãn
Từ hai trường hợp trên, các giá trị của thỏa mãn là:
m = 0,1,2.
Bước 4: Tính tổng bình phương các giá trị của
Tổng bình phương các giá trị m là:
S = 02 + 12 + 22
Tính:
S = 0 + 1 + 4 = 5
—
Kết luận
Tổng bình phương các giá trị nguyên của m để hàm số nghịch biến trên R là:
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129652
Đã trả lời bởi chuyên gia
129652 -
 Đã trả lời bởi chuyên gia
104087
Đã trả lời bởi chuyên gia
104087 -
 Đã trả lời bởi chuyên gia
94063
Đã trả lời bởi chuyên gia
94063 -
 Đã trả lời bởi chuyên gia
69340
Đã trả lời bởi chuyên gia
69340



