Quảng cáo
2 câu trả lời 15150
Giải bài toán: Khoảng cách từ A đến mặt phẳng (SCD)
1. Tóm tắt bài toán
Cho hình chóp tứ giác đều S.ABCD với:
- Cạnh đáy AB = BC = CD = DA = 2a,
- Chiều cao của hình chóp
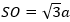 , với O là tâm của hình vuông đáy ABCD,
, với O là tâm của hình vuông đáy ABCD, - Cần tìm khoảng cách từ điểm A đến mặt phẳng (SCD).
2. Phân tích lời giải
Khoảng cách từ điểm A đến mặt phẳng (SCD) được tính dựa trên khoảng cách từ O đến mặt phẳng (SCD), với O là tâm của đáy ABCD.
Theo lời giải trong hình:
![]()
Khi đó, khoảng cách từ O đến mặt phẳng (SCD) có công thức:
![]()
trong đó:
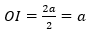 (nửa đường chéo của hình vuông đáy ),
(nửa đường chéo của hình vuông đáy ), (chiều cao của hình chóp).
(chiều cao của hình chóp).
3. Tính khoảng cách ![]()
Thay các giá trị vào công thức:
![]()
Cụ thể:

Rút gọn mẫu số:
![]()
Do đó:
![]()
4. Tính khoảng cách từ A đến mặt phẳng (SCD)
Ta có:
![]()
Thay ![]() , ta được:
, ta được:
![]()
5. Kết luận
Khoảng cách từ A đến mặt phẳng (SCD) là:
![]()
Đáp án đúng là: C. ![]() .
.
Mỵ Nguyễn Thị
· 2 năm trước
Tại sao đoạn đầu A lại bằng 2 lần O vậy ạ. Kiến thức này ở đâu vậy ạ sao e kbt . Mong ad chỉ cho e với
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129637
Đã trả lời bởi chuyên gia
129637 -
 Đã trả lời bởi chuyên gia
104061
Đã trả lời bởi chuyên gia
104061 -
 Đã trả lời bởi chuyên gia
94054
Đã trả lời bởi chuyên gia
94054 -
 Đã trả lời bởi chuyên gia
69272
Đã trả lời bởi chuyên gia
69272
Gửi báo cáo thành công!




