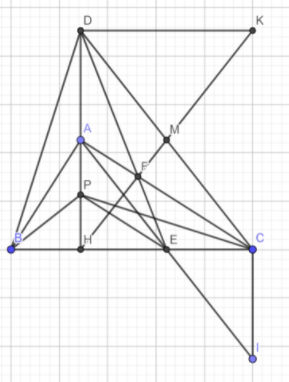
Cho tam giác ABC vuông tại A, đường cao AH. Trên tia đối của tia AH lấy điểm D sao cho AD = AH. Gọi E là trung điểm của HC, M là trung điểm của DC, F là giao điểm của DE và AC.
a, Chứng minh 3 điểm H, F, M thẳng hàng
b, Chứng minh HF = DC
c, Qua E kẻ đường thẳng vuông góc với AB cắt AH tại P. Chứng minh CPBD.
Quảng cáo
1 câu trả lời 12457



Nguyễn Huyền CHI
· 2 năm trước
Cho tam giác ABC vuông góc với A đường cao AH Trên tia đối của tia ah lấy điểm D sao cho AB = ah điểm D thuộc đường đoạn thẳng của AC sao cho CF = 2 AF a) chứng minh điểm F là trung tâm của tam giác DCH b) đường thẳng hs cắt đường thẳng CD tại M cho HF=2cm ,Tính HM c) qua đê đường thẳng song song với BC cắt đường thẳng HM tại điểm I . Chứng minh tam giác dhe = tam giác cmh d) Chứng minh D vuông góc với HD và hf = 1/3 DC
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK121162
-
 Đã trả lời bởi chuyên gia
81971
Đã trả lời bởi chuyên gia
81971 -
 Đã trả lời bởi chuyên gia
59862
Đã trả lời bởi chuyên gia
59862 -
 Đã trả lời bởi chuyên gia
39757
Đã trả lời bởi chuyên gia
39757
Gửi báo cáo thành công!


