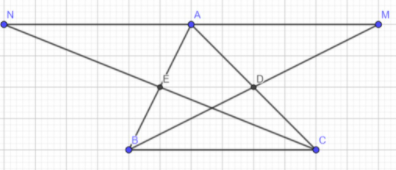
Cho tam giác ABC, gọi D là trung điểm của AC. Gọi E là trung điểm của AB. Trên tia đối của tia DB lấy điểm M sao cho Dm = DB. Trên tia đối của tia EC lấy điểm N sao cho EN = EC. Chứng minh A là trung điểm của MN.
Quảng cáo
2 câu trả lời 11335
a/ Xét ΔADMΔADM và ΔCDBΔCDB có:
AD=CD(vì d là trung điểm của AC)
ˆADM=ˆCDMADM^=CDM^ (2 góc đối đỉnh)
DM=DB(gt)
⇒ΔADM=ΔCDB(c.g.c)⇒ΔADM=ΔCDB(c.g.c)
⇒ˆMAD=ˆBCD⇒MAD^=BCD^ (2 góc tương ứng bằng nhau), AM=CB( 2 cạnh tương ứng bằng nhau)
Mà ˆMADMAD^ và ˆBCDBCD^ ở vị trí so le trong
⇒⇒ AM//BC (1)
Xét ΔNAEΔNAE và ΔCBEΔCBE có:
AE=BE(vì E là trung điểm của AB)
ˆNEA=ˆCEBNEA^=CEB^ (2 góc đối đỉnh)
NE=CE(gt)
⇒ΔNAE=ΔCBE(c.g.c)⇒ΔNAE=ΔCBE(c.g.c)
⇒ˆNAE=ˆCBE⇒NAE^=CBE^ (2 góc tương ứng bằng nhau), NA=CB(2 cạnh tương ứng bằng nhau)
Mà ˆNAENAE^ và ˆCBECBE^ ở vị trí so le trong
⇒⇒ NA//BC (2)
Ta thấy (1) và (2) mâu thuẫn vì qua một điểm nằm ngoài một đường thẳng chỉ kẻ được một đường thẳng duy nhất song song với đường thẳng ấy nên ba điểm N , A , M thẳng hàng (3)
Mặt khác: AM=CB(cmt)
NA=CB(cmt)
⇒⇒ AM=NA (4)
Từ (3) và (4) ⇒⇒ A là trung điểm của MN
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120761
-
81498
-
59515