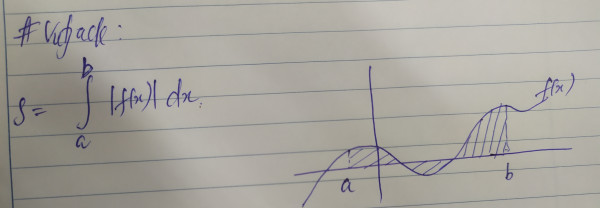
Hình phẳng (H) được giới hạn bởi đồ thị hàm số f(x) liên tục trên đoạn [a,b] trục hoành hai đường thảng x=a ,x=b.khi đó diện tích S của hình phảng (H) đuoc tính theo công thức là
Quảng cáo
2 câu trả lời 507
1. Tình huống
Hàm số f(x)f(x)f(x) liên tục trên đoạn [a,b][a, b][a,b].
Hình phẳng HHH được giới hạn bởi:
Đường cong y=f(x)y = f(x)y=f(x)
Trục hoành y=0y = 0y=0
Hai đường thẳng x=ax = ax=a và x=bx = bx=b
2. Diện tích hình phẳng
Nếu hàm số luôn không âm trên đoạn [a,b][a, b][a,b] (f(x)≥0f(x) \ge 0f(x)≥0), diện tích hình phẳng được tính bằng tích phân xác định:
S=∫abf(x) dxS = \int_{a}^{b} f(x) \, dxS=∫abf(x)dxNếu f(x)≤0f(x) \le 0f(x)≤0 trên một phần nào đó của đoạn [a,b][a, b][a,b], thì diện tích vẫn luôn là giá trị tuyệt đối của tích phân, vì diện tích luôn dương:
S=∫ab∣f(x)∣ dxS = \int_a^b |f(x)| \, dxS=∫ab∣f(x)∣dx
3. Ghi chú
Đây là công thức cơ bản trong tích phân xác định.
Nếu đồ thị cắt trục hoành, ta cần chia đoạn [a,b][a,b][a,b] ra thành các phần mà hàm luôn đồng dấu, rồi tính tổng diện tích các phần:
S=∫ac1∣f(x)∣ dx+∫c1c2∣f(x)∣ dx+⋯+∫cn−1b∣f(x)∣ dxS = \int_{a}^{c_1} |f(x)|\,dx + \int_{c_1}^{c_2} |f(x)|\,dx + \dots + \int_{c_{n-1}}^{b} |f(x)|\,dxS=∫ac1∣f(x)∣dx+∫c1c2∣f(x)∣dx+⋯+∫cn−1b∣f(x)∣dxvới c1,c2,…,cn−1c_1, c_2, \dots, c_{n-1}c1,c2,…,cn−1 là các giao điểm với trục hoành (f(x)=0f(x) = 0f(x)=0).
✅ Tóm tắt:
Nếu f(x)≥0f(x) \ge 0f(x)≥0 trên [a,b][a,b][a,b]:
S=∫abf(x) dx\boxed{S = \int_a^b f(x)\,dx}S=∫abf(x)dxNếu f(x)f(x)f(x) đổi dấu:
S=∫ab∣f(x)∣ dx\boxed{S = \int_a^b |f(x)|\,dx}S=∫ab∣f(x)∣dx
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129652
Đã trả lời bởi chuyên gia
129652 -
 Đã trả lời bởi chuyên gia
104087
Đã trả lời bởi chuyên gia
104087 -
 Đã trả lời bởi chuyên gia
94063
Đã trả lời bởi chuyên gia
94063 -
 Đã trả lời bởi chuyên gia
69340
Đã trả lời bởi chuyên gia
69340