Giải bài toán tiệm cận của hàm số
Phân tích bài toán
Hàm số đã cho:

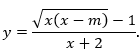
Mục tiêu: Xác định các giá trị  nguyên thuộc khoảng (-10; 10) sao cho đồ thị hàm số có đúng 3 đường tiệm cận.

Điều kiện để có 3 đường tiệm cận
Bước 1: Xét điều kiện của hàm số

- Hàm số có dạng phân thức với mẫu số x + 2, nên hàm số không xác định tại:

x = -2

Đây là một tiệm cận đứng nếu tử số xác định tại x = -2.

Bước 2: Xét tiệm cận ngang

- Tiệm cận ngang phụ thuộc vào bậc của tử số và mẫu số khi : - Tử số: -1 khi x $\to \infty$ có bậc là 1 (do x(x - m) chứa x², nhưng căn bậc hai làm giảm bậc đi 1). - Mẫu số: x + 2 cũng có bậc 1.

Do bậc của tử số và mẫu số đều là 1, hàm số có tiệm cận ngang khi :

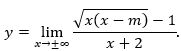
Khi phân tích tử số và mẫu số:

- Với :

- Với :

Do đó, hàm số có 2 tiệm cận ngang y = 1 và y = -1.

Bước 3: Điều kiện để có tiệm cận đứng tại x = -2

Hàm số sẽ có tiệm cận đứng tại x = -2 nếu tử số xác định và khác 0 tại x = -2.

Thay x = -2 vào tử số:

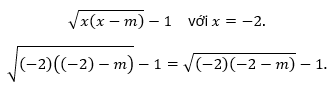
Để biểu thức dưới dấu căn xác định (không âm), ta cần:

Giải bất phương trình:

Tổng hợp các điều kiện
Từ các phân tích trên, để hàm số có đúng 3 tiệm cận, cần thỏa mãn các điều kiện:

• m $\ge -2$ để có tiệm cận đứng tại x = -2,
•  thuộc khoảng (-10; 10),
• m là số nguyên.

Xác định số giá trị m
Các giá trị m nguyên thỏa mãn:

Dãy số nguyên m là:

Số các giá trị m là 12.

Kết luận
Số giá trị m nguyên thuộc khoảng (-10; 10) để hàm số có đúng 3 đường tiệm cận là:

Đáp án đúng: A. 12.