a, Chứng minh M, P lần lượt là trung điểm của AB, AC
b, Tứ giác ANCE là hình gì ?
Quảng cáo
1 câu trả lời 35
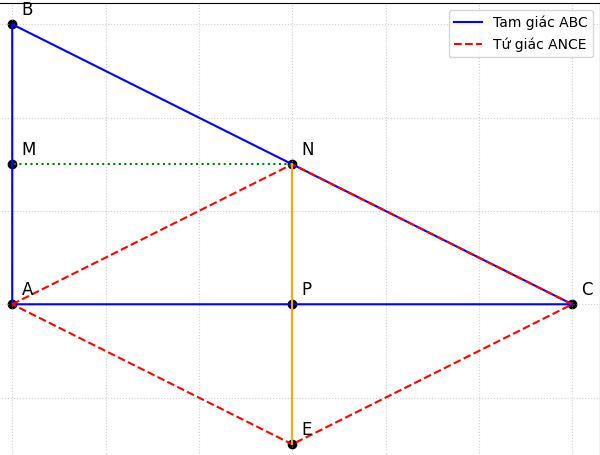
a. Chứng minh M, P lần lượt là trung điểm của AB, AC
- Xét ABC vuông tại A:
* Chứng minh M là trung điểm AB:
Ta có NM AB (vì M là hình chiếu của N lên AB).
Mà AC AB (giả thiết tam giác vuông tại A).
=> NM // AC.
- Xét ABC có N là trung điểm của BC và NM // AC. Theo định lý đường trung bình của tam giác, đường thẳng đi qua trung điểm một cạnh và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
=> Vậy M là trung điểm của $AB$.
* Chứng minh P là trung điểm AC:
- Tương tự, ta có NP AC (vì P là hình chiếu của N lên AC).
Mà AB AC.
=> NP // AB.
Xét ABC có N là trung điểm của BC và NP // AB.
Vậy P là trung điểm của AC.
b. Tứ giác ANCE là hình gì?
- Để xác định tứ giác ANCE, ta xét hai đường chéo AC và NE:
- Xét các yếu tố của tứ giác:
+ Ta có P là trung điểm của AC (chứng minh ở câu a).
+ Theo giả thiết, P là trung điểm của NE.
=> Tứ giác ANCE có hai đường chéo AC và NE cắt nhau tại trung điểm P của mỗi đường.
Do đó, ANCE là một hình bình hành.
- Xét tính chất vuông góc:
+ Ta có NP AC (vì P là hình chiếu của N lên AC).
=> NE AC tại P.
- Một hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
Vậy: Tứ giác ANCE là hình thoi.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
108331
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
69198
Đã trả lời bởi chuyên gia
69198 -
 Đã trả lời bởi chuyên gia
53156
Đã trả lời bởi chuyên gia
53156 -
 Đã trả lời bởi chuyên gia
47629
Đã trả lời bởi chuyên gia
47629 -
 Đã trả lời bởi chuyên gia
45789
Đã trả lời bởi chuyên gia
45789 -
 Đã trả lời bởi chuyên gia
45534
Đã trả lời bởi chuyên gia
45534 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
39114
Đã trả lời bởi chuyên gia
39114 -
 Đã trả lời bởi chuyên gia
38468
Đã trả lời bởi chuyên gia
38468


