Cho tam giác ABC có ba góc nhọn, trực tâm H. Một đường thẳng đi qua H, cắt AB, AC ở P, Q sao cho HP = HQ. Gọi M là trung điểm của BC. Qua C vẽ đường song song với PQ, cắt AB ở N, AH ở K . Chứng minh:
a) H là trực tâm tam giác CK M.
b) MP = MQ
Quảng cáo
1 câu trả lời 70
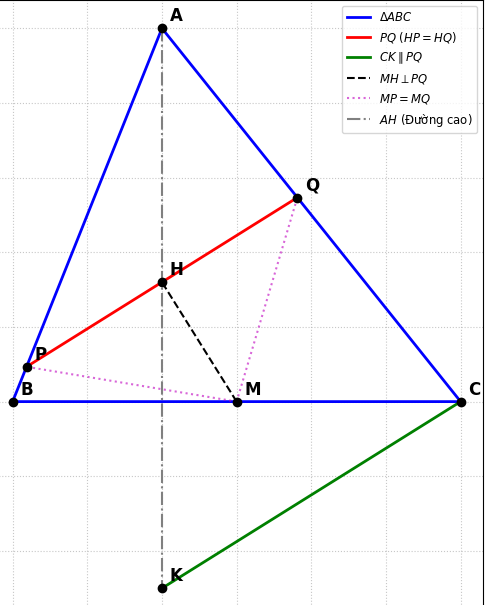
a) Chứng minh H là trực tâm tam giác CKM
- Ta có các nhận xét quan trọng sau:
H là trực tâm tam giác ABC ⇒ AH ⊥ BC
M là trung điểm của BC ⇒ HM ⊥ BC
=> HM ⊥ CK(vì CK // PQ, PQ ⊥ BC)
- Tiếp theo: CK // PQ mà PQ đi qua H
=> CK ⊥ HM
Mặt khác: AH ⊥ BC, M ∈ BC ⇒ AH ⊥ CM
Mà K ∈ AH nên: HK ⊥ CM
⟹ H là giao điểm của hai đường cao trong tam giác CKM
=> H là trực tâm tam giác CKM (đpcm)
b) Chứng minh MP = MQ
- Ta có:
HP = HQ (giả thiết)
M là trung điểm của BC
HM ⊥ BC
- Xét hai tam giác: △HMP và △HMQ, ta có:
HP = HQ
HM chung
= = 90∘
⟹ Hai tam giác △HMP và △HMQ bằng nhau (cạnh–góc–cạnh)
=> MP = MQ (đpcm)
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
108331
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
69198
Đã trả lời bởi chuyên gia
69198 -
 Đã trả lời bởi chuyên gia
53156
Đã trả lời bởi chuyên gia
53156 -
 Đã trả lời bởi chuyên gia
47629
Đã trả lời bởi chuyên gia
47629 -
 Đã trả lời bởi chuyên gia
45789
Đã trả lời bởi chuyên gia
45789 -
 Đã trả lời bởi chuyên gia
45534
Đã trả lời bởi chuyên gia
45534 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
39114
Đã trả lời bởi chuyên gia
39114 -
 Đã trả lời bởi chuyên gia
38468
Đã trả lời bởi chuyên gia
38468


