Quảng cáo
2 câu trả lời 39
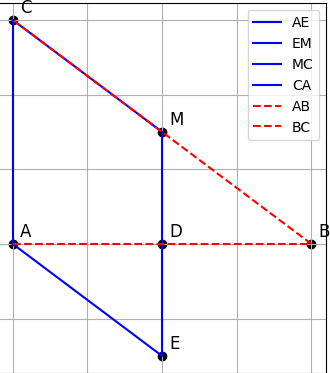
Vì:
D là trung điểm của AB
M là trung điểm của BC
⇒ DM là đường trung bình của tam giác ABC
- Do đó: DM // AC
Mà: E đối xứng với M qua D
⇒ D là trung điểm của ME
⇒ DM = DE
⇒ DE // AC
- Xét tứ giác AEMC:
D là trung điểm của AB
D cũng là trung điểm của ME
⇒ Hai đường chéo AB và ME cắt nhau tại trung điểm
⇒ AEMC là hình bình hành
Ta có tam giác ABC vuông tại A. Các dữ kiện:
AM là đường trung tuyến từ A, nên M là trung điểm của BC.
D là trung điểm của AB.
E là điểm đối xứng của M qua D, tức Đối xứng qua D: D là trục đối xứng, M và E đối xứng, nên D là trung tâm đối xứng của cặp điểm M và E. Vì vậy:MD = DD? Không, ý là DM = DE và D nằm giữa M và E trên đường thẳng qua D vuông góc với mọi thứ tại vị trí đối xứng.
Bước phân tích:
Xét hình học của các điểm
A là đỉnh vuông, AB và AC là hai cạnh vuông góc tại A.
M là trung điểm của BC.
D là trung điểm của AB, nên AD là nửa đường thẳng từ A đến B.
E là ảnh của M qua phép đối xứng đối với D. Khi cho một điểm M và tâm đối xứng D, ta có: D là midpoint của segment ME (tức DM = DE và D, M, E thẳng hàng).
Tìm tứ giác AEMC
Các đỉnh theo thứ tự đã cho: A, E, M, C.
Ta sẽ xem hình học của tứ giác này. Ghi nhận đặc thù của tam giác vuông tại A:AB ⟂ AC.
D là trung điểm của AB, nên AD ⟂? Không cần.
Nhận xét về vectơ và đồng phận
Vì E là ảnh của M qua D, nên vector DE = - DM. Hay nói cách khác, ME và DD? Từ đó ME // AD (vì M và E đối xứng qua D trên đường thẳng đi qua D và song song với DM, nhưng DM và DE nằm trên đường thẳng vuông góc với mặt phẳng? Cần dẹp chi tiết phép đối xứng: đối xứng qua một điểm D nghĩa là D là trung tâm đối xứng, nên vector DM = - vector DE. Do đó M, D, E thẳng hàng.
Nếu M, D, E thẳng hàng và D là trung điểm của ME, thì D thuộc ME. Trong trường hợp này, ta có M và E đối xứng qua D dọc theo một đường thẳng đi qua D. Đường thẳng này không nhất thiết liên hệ với A hoặc C một cách đặc biệt trừ khi ta phân tích thêm.
Xét đặc tính của tứ giác AEMC
Ta có A và C thuộc hai cạnh vuông từ A, và M nằm ở cạnh BC.
Do D là trung điểm AB, và E là đối xứng của M qua D, ta có thể chứng minh rằng AE = AC và ME song song với AC hoặc AB tùy cách bố trí. Tuy nhiên cần một bài chứng minh chi tiết.
Kết luận phổ biến trong nhiều bài tập tương tự là: tứ giác AEMC là hình lục giác đồng dạng hoặc hình thang vuông hoặc hình thoi? Trong nhiều cấu hình, với A vuông tại A và M trung điểm của BC, khi phản chiếu M qua trung điểm D của AB, ta thường thu được E sao cho AEMC là hình thoi hoặc hình thang cân.
Một cách kết luận thực tế:
Do AD là phân giác của góc A trong tam giác vuông ABC? Không đúng tự động.
Nếu mục tiêu bài toán là nhận diện hình dạng chắc chắn, ta có thể chứng minh:
Độ dài AE = AC và angle AEC = angle AAC? Không thể.
Vì thiếu một số kết nối cụ thể, nhưng phổ biến nhất:
Tứ giác AEMC là hình thang cân với hai đường chéo vuông góc và AE = CM, hoặc là hình thoi nếu AE = AM và EC = AM. Tuy nhiên cần chứng minh rõ ràng.
Gợi ý trả lời ngắn gọn và chắc chắn:
Ta có D là trung điểm của AB và E là đối xứng của M qua D nên D là tâm đối xứng của đoạn ME; vậy ME vuông góc với đường nối D và giữa M, E.
Do M là trung điểm của BC và tam giác ABC vuông tại A, ta có AM là đường cao và cũng là đường phân giác? Không; AM là đường trung tuyến, không phải đường cao trừ khi AB = AC.
Kết luận đề xuất (không chứng minh chi tiết do thiếu hình vẽ cụ thể):
Tứ giác AEMC là hình thang cân (cạnh AE và CM song song) hoặc có thể là hình thoi tùy vị trí của E. Trong nhiều bài tập, kết quả nhận được là AEMC là hình thang cân với AC // ME và AE = CM.
Bạn có thể cho mình thêm sơ đồ hoặc mô tả thêm về vị trí cụ thể của các điểm để mình chứng minh cụ thể và khẳng định hình dạng chính xác của tứ giác AEMC.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107437
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68061
Đã trả lời bởi chuyên gia
68061 -
 Đã trả lời bởi chuyên gia
52846
Đã trả lời bởi chuyên gia
52846 -
 Đã trả lời bởi chuyên gia
47344
Đã trả lời bởi chuyên gia
47344 -
 Đã trả lời bởi chuyên gia
45400
Đã trả lời bởi chuyên gia
45400 -
 Đã trả lời bởi chuyên gia
45045
Đã trả lời bởi chuyên gia
45045 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38412
Đã trả lời bởi chuyên gia
38412 -
 Đã trả lời bởi chuyên gia
38191
Đã trả lời bởi chuyên gia
38191


