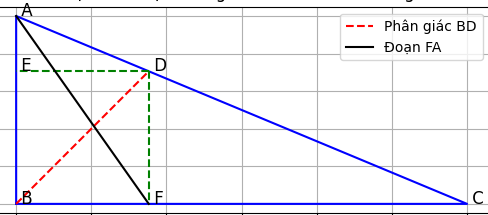
Cho tam giác ABC vuông tại B, BD là tia phân giác của góc ABC ( D thuộc AC). Gọi E, F lần lượt là hình chiếu vuông góc của D trên cạnh AB, BC.
a) Tứ giác BEDF là hình gì? Vì sao?
b) Cho AC=13cm, AB=5cm, BC = 12cm Tính AD, DC.
C) FA cắt BD tại M, cắt ED tại N. Chứng minh
Quảng cáo
1 câu trả lời 59
Giải bài toán
a) Tứ giác BEDF là hình gì? Vì sao?
Xét tứ giác BEDF có:
= 90 (do tam giác ABC vuông tại B).
= 90 (E là hình chiếu của D lên AB).
= 90 (F là hình chiếu của D lên BC).
=> Tứ giác BEDF là hình chữ nhật (tứ giác có 3 góc vuông).
- Mặt khác, BD là tia phân giác của góc , nên theo tính chất tia phân giác, điểm D cách đều hai cạnh AB và BC.
=> DE = DF.
=> Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông. Vậy BEDF là hình vuông.
b) Tính AD và DC
- Theo tính chất đường phân giác trong tam giác ABC:
- Áp dụng tính chất tỉ lệ thức:
=> AD =
=> DC =
c) Chứng minh
- Vì BEDF là hình vuông nên ED // BC và EN // BF.
- Xét tam giác ABF có EN // BF, theo hệ quả định lý Thales:
- Vì ED // BC, theo định lý Thales trong tam giác ABC: (2)
Thay vào (1), và vì ED = BF (cạnh hình vuông), ta có: (3)
- Từ (3) mà ED = BF = a (cạnh hình vuông) => (4)
- Xét tam giác ABF có EN // BF, theo hệ quả Thales: (5)
- Thay (2) vào (5) ta được:
- Xét tam giác ABM có DF // AB (do BEDF là hình vuông), theo hệ quả định lý Thales:
Kết hợp với (*), ta có:
=> Áp dụng tính chất tỉ lệ thức:
=> Chia cả hai vế cho FA, ta được đpcm:
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107437
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68061
Đã trả lời bởi chuyên gia
68061 -
 Đã trả lời bởi chuyên gia
52846
Đã trả lời bởi chuyên gia
52846 -
 Đã trả lời bởi chuyên gia
47344
Đã trả lời bởi chuyên gia
47344 -
 Đã trả lời bởi chuyên gia
45400
Đã trả lời bởi chuyên gia
45400 -
 Đã trả lời bởi chuyên gia
45045
Đã trả lời bởi chuyên gia
45045 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38412
Đã trả lời bởi chuyên gia
38412 -
 Đã trả lời bởi chuyên gia
38191
Đã trả lời bởi chuyên gia
38191


