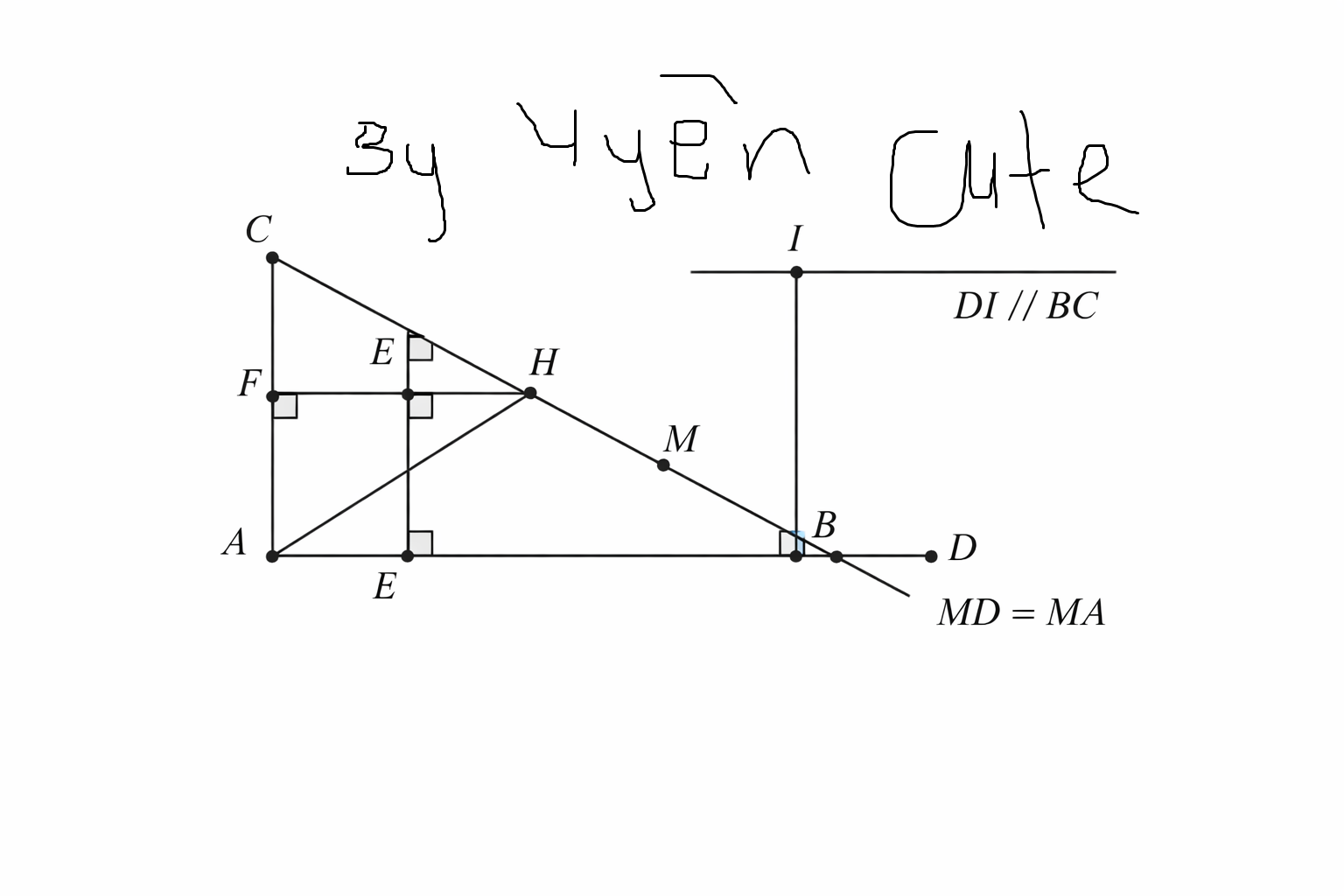
Bài 5. Cho tam giác ABC vuông tại A ( AB < AC), trung tuyến AM, đường cao AH. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a) Tứ giác ABDC là hình gì? Vì sao.
b) Qua điểm D kẻ đường thẳng song song với BC, đường thẳng này cắt tia AH tại I .
Chứng minh BC là đường trung trực của AI.
c) Chứng minh tứ giác BIDC là hình thang cân.
d) Kẻ HE AB tại E, HF AC tại F. Chứng minh EF AM
Quảng cáo
3 câu trả lời 90
 ài giải
ài giải
Cho tam giác ABC vuông tại A (AB < AC), AM là trung tuyến, AH là đường cao.
Lấy điểm D trên tia đối của tia MA sao cho MD = MA.
a) Chứng minh tứ giác ABDC là hình gì?
Ta có:
M là trung điểm của BC (vì AM là trung tuyến).
MD = MA nên M là trung điểm của AD.
Vậy trong tứ giác ABDC, hai đường chéo AD và BC cắt nhau tại M và cắt nhau tại trung điểm mỗi đường.
⇒ ABDC là hình bình hành.
b) Qua D kẻ đường thẳng song song với BC, cắt tia AH tại I.
Chứng minh BC là đường trung trực của AI.
Ta có:
DI song song với BC (theo cách dựng).
AH vuông góc với BC (vì AH là đường cao).
⇒ AH cũng vuông góc với DI tại I.
Xét tam giác ADI:
M là trung điểm của AD
AH vuông góc AD tại I
⇒ BC đi qua M và vuông góc với AI.
Vậy BC là đường trung trực của AI.
c) Chứng minh tứ giác BIDC là hình thang cân
Ta có:
DI song song BC ⇒ BIDC là hình thang.
BC là đường trung trực của AI ⇒ BI = CI.
Hình thang có hai cạnh bên bằng nhau là hình thang cân.
⇒ BIDC là hình thang cân.
d) Kẻ HE vuông góc AB tại E, HF vuông góc AC tại F.
Chứng minh EF song song AM.
Ta có:
HE vuông góc AB
HF vuông góc AC
AB vuông góc AC (tam giác ABC vuông tại A)
⇒ HE song song AC, HF song song AB.
Suy ra tứ giác AEHF là hình chữ nhật.
Trong hình chữ nhật, các đường nối trung điểm hai cạnh đối song song với đường chéo.
Mà AM là đường chéo của hình chữ nhật AEHF.
⇒ EF song song AM.
Kết luận:
a) ABDC là hình bình hành
b) BC là đường trung trực của AI
c) BIDC là hình thang cân
d) EF song song AM
 ko biết làm
ko biết làm
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
107278
-
Hỏi từ APP VIETJACK67830
-
44998
-
38171


