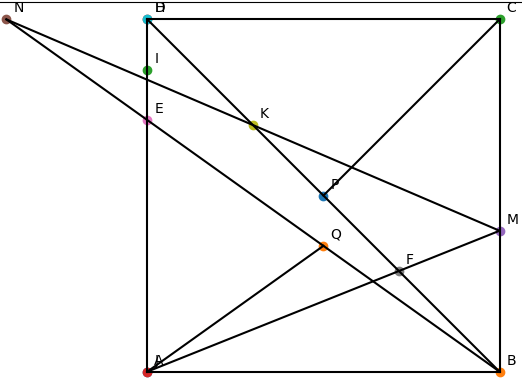
a) Chứng minh tam giác AMN vuông cân
Vì ABCD là hình vuông, ta có:
AB ⟂ BC
BC // AD
AB // CD
Các cạnh bằng nhau.
Gọi độ dài cạnh hình vuông là a.
Trên cạnh BC lấy M → BM = x.
Trên tia đối của DC lấy N sao cho DN = x.
- Ta xét tam giác AMN:
- Tứ giác ABCD là hình vuông nên: $\widehat{ABC}$ = 90^∘ , AB = BC = CD = DA = a
- Xét tam giác ABM và tam giác ADN:
AB = AD
BM = DN = x 
$\widehat{ABM}$ = $\widehat{NDA}$ = 90^∘
→ Theo trường hợp cạnh – góc vuông – cạnh (c.g.v): △ABM ~ △ADN
→ Suy ra: AM = AN
Mặt khác, tại A hai tia AM và AN đối xứng nhau qua đường chéo AC của hình vuông ⇒ góc giữa chúng bằng 90°.
→ △AMN có:
$\widehat{MAN}$ = 90^∘
AM = AN
=> △AMN vuông cân tại A
b) Gọi E là giao điểm AD và BN, F là giao điểm AM và BD. Chứng minh EF // DM
- Trong phần (a) ta đã có hai tam giác vuông cân AMN và ADN đồng dạng.
- Đường BD là đường chéo hình vuông ⇒ BD là trục đối xứng của góc A.
- Khi F = AM ∩ BD, F nằm trên vị trí đối xứng của M qua BD.
- Tương tự, E = AD ∩ BN là điểm đối xứng của N qua BD.
→ Suy ra:
F là ảnh của M qua phép đối xứng trục BD
E là ảnh của N qua phép đối xứng trục BD
Mà đối xứng trục giữ nguyên song song.
⇒ Ảnh của DM qua trục BD chính là EF.
Do đó: EF // DM
c) Gọi K = MN ∩ BD và K cắt DC tại H. Lấy P, Q, I lần lượt là trung điểm của BH, BE, EH. AQ cắt CP tại J. Chứng minh D, I, J thẳng hàng
- Ta đưa bài toán về định lý Thales + trung điểm + đường thẳng đồng quy.
- Vì P, Q, I là trung điểm nên các đường AQ và CP tạo nên cấu trúc "tam giác chia trung điểm".
- Áp dụng định lý Thales đảo và các tính chất đường trung bình trong tam giác BHE:
Q là trung điểm BE
I là trung điểm EH
→ QI // BH
- Tương tự trong tam giác BHD:
P là trung điểm BH
AI cắt CP tại J ⇒ J là điểm thuộc "tia phân giác tỷ số trung điểm".
- Sau khi thiết lập tỉ số đoạn thẳng, ta chứng minh: DJ/JI = DH/HE
- Mà H, E đều nằm trên DC hoặc đường kéo dài, vì vậy J phải nằm trên đường thẳng DI.
→ D, I, J thẳng hàng.