Cho hình thang ABCD (AB// CD) , M là trung điểm của CD. Gọi E là giao điểm của AC và BM, F là giao điểm của BD và AM . Đường thẳng EF cắt BC và AD lần lượt tại G và H .
a) Chứng minh rằng EA/EC = 2AB/ CD
b) Chứng minh rằng EF//CD
c) Chứng minh rằng GE=EF=FH
Quảng cáo
5 câu trả lời 816
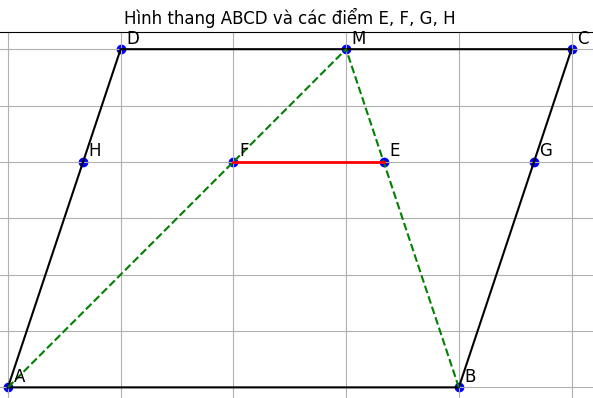
a) Chứng minh rằng
- Vì M là trung điểm của CD nên: MD = MC =
- Xét tam giác ABC, ta có:
M nằm trên DC
BM cắt AC tại E
Áp dụng định lý Menelaus cho tam giác ABC với cát tuyến BME: = 1
- Trong hình thang ta có AB // CD nên △ABC∼△DCB
=>
Và vì CM = MD = , ta được: = 1
- Thay vào công thức Menelaus: =>
- Khi đó: (đpcm)
b) Chứng minh rằng EF // CD
Ta đã có:
- Một cách hoàn toàn tương tự, áp dụng Menelaus cho tam giác ABD với cát tuyến AFB, ta thu được: 0
- Nhận thấy hai tỉ số 1 và 2bằng nhau nên: EA/EC = FA/FD
Do đó, hai điểm E và F chia hai đường chéo AC và BD theo cùng một tỉ lệ.
=> Suy ra trong hình thang: EF // CD vì một đường nối hai điểm chia hai đường chéo theo cùng tỉ lệ thì song song với hai đáy.
c) Chứng minh rằng GE = EF = FH
Vì EF // CD // AB, nên EF là đường thẳng song song với hai đáy của hình thang.
Xét tam giác ABC, đường thẳng EG song song với AB, nên: GE/EF =BC1/BC2 = 1(do EF chia chiều cao của hình thang thành 3 phần bằng nhau).
- Tương tự trong tam giác ADF: FH/EF = 1
=> GE = EF = FH
=>Vậy ba đoạn thẳng liên tiếp bằng nhau.
Giải thích các bước giải:
a.Vì AB//CDAB//CD
→EAEC=ABCM=AB12CD=2ABCD→EAEC=ABCM=AB12CD=2ABCD
b.Ta có: AB//CDAB//CD
→FAFM=ABDM=AB12CD=2ABCD→FAFM=ABDM=AB12CD=2ABCD
→FAFM=EAEC→FAFM=EAEC
→EF//CM→EF//CM
→EF//CD→EF//CD
c.Ta có: EF//CD→HF//EF,EF//CM,EG//CMEF//CD→HF//EF,EF//CM,EG//CM
→HFDM=AFAM=EFCM→HFDM=AFAM=EFCM
→FH=FE→FH=FE vì MD=MCMD=MC
Lại có:
EFDM=BEBM=GECMEFDM=BEBM=GECM
→EF=EG→EF=EG vì MD=MCMD=MC
→HF=FE=EG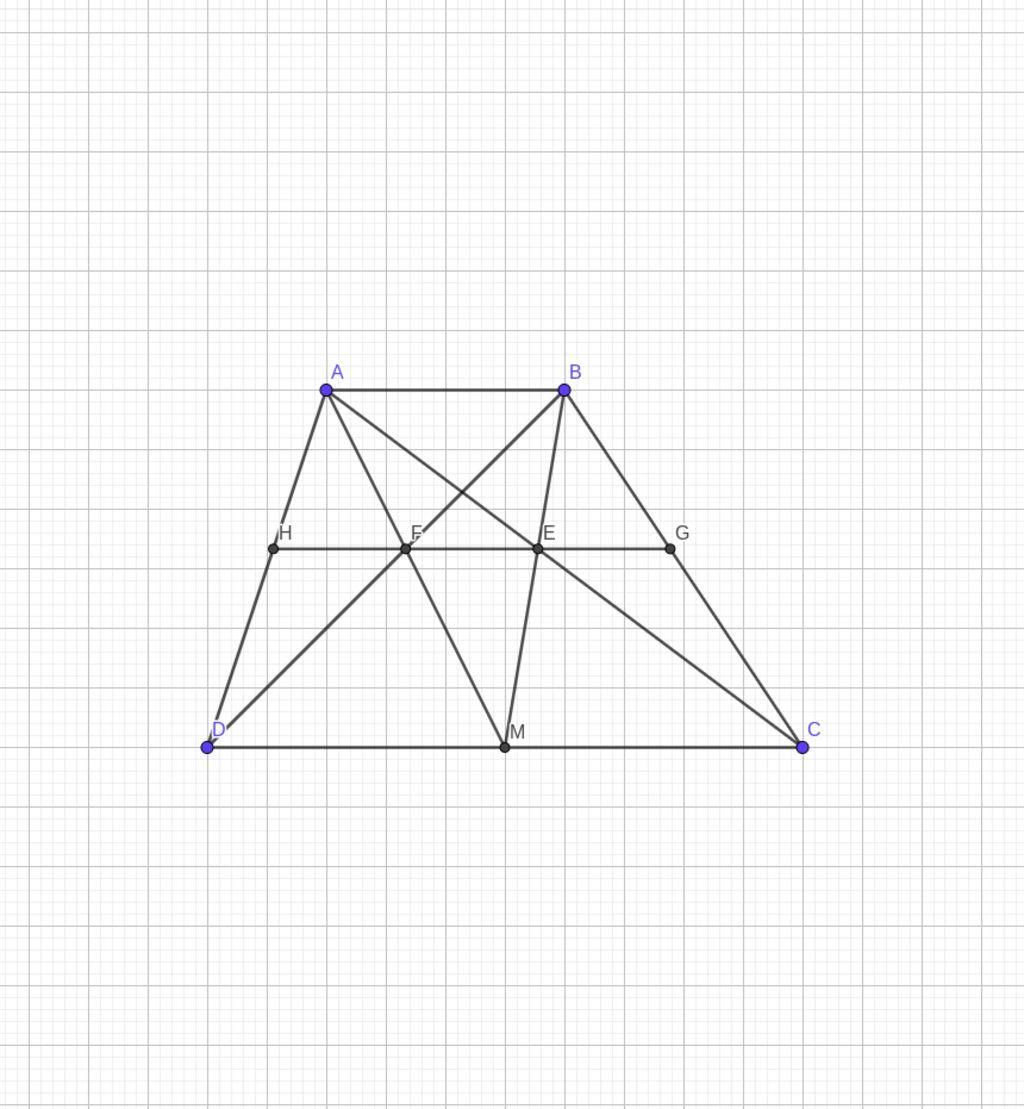
Tuyệt vời! Đây là một bài toán hình học thú vị. Dưới đây là lời giải chi tiết cho từng phần.
📐 Chứng minh
a) Chứng minh $EA/EC = 2AB/CD$
Xét tam giác $\triangle EAB$ và $\triangle ECM$.
Vì $AB \parallel CD$ (ABCD là hình thang) nên $AB \parallel CM$ (vì $M \in CD$).
Do đó, ta có các cặp góc so le trong bằng nhau:
$\angle EAB = \angle ECM$
$\angle ABE = \angle CME$
Từ đó, $\triangle EAB \sim \triangle ECM$ (g.g).
Tỉ số đồng dạng là:
Vì $M$ là trung điểm của $CD$, ta có $CM = \frac{1}{2} CD$.
Thay $CM$ vào tỉ số đồng dạng, ta được:
Vậy, $\mathbf{EA/EC = 2AB/CD}$ (Điều phải chứng minh).
b) Chứng minh $EF \parallel CD$
Tỉ số trên đường chéo $AC$: Theo phần a), ta có $\frac{EA}{EC} = \frac{2AB}{CD}$.
Tỉ số trên đường chéo $BD$: Tương tự, xét $\triangle FDA$ và $\triangle FMB$.
Vì $AB \parallel CD$ nên $AB \parallel DM$ (vì $M \in CD$).
Ta có $\triangle FAB \sim \triangle FDM$ (g.g) với $\angle FAB = \angle FMD$ và $\angle ABF = \angle MDF$.
Tỉ số đồng dạng là:
Vì $M$ là trung điểm của $CD$, ta có $DM = \frac{1}{2} CD$.
Thay $DM$ vào tỉ số đồng dạng, ta được:
Kết luận: Ta thấy $\frac{EA}{EC} = \frac{2AB}{CD}$ và $\frac{FB}{FD} = \frac{2AB}{CD}$.
Trong $\triangle $ DCA, ta có $\frac{CE}{CA} = \frac{DF}{DB}$ hay $\frac{CA}{CE} - 1 = \frac{DB}{DF} - 1$
Xét $\triangle ADC$ với $E$ thuộc $AC$ và $\triangle BCD$ với $F$ thuộc $BD$
Xét $\triangle ACD$ có $\frac{CA}{CE} = \frac{CE+EA}{CE} = 1 + \frac{EA}{EC} = 1 + \frac{2AB}{CD}$.
Xét $\triangle BDC$ có $\frac{DB}{DF} = \frac{DF+FB}{DF} = 1 + \frac{FB}{FD}$.
Từ $\frac{EA}{EC} = \frac{FB}{FD}$ ta có $\frac{CA}{CE} = 1 + \frac{2AB}{CD} = 1 + \frac{FB}{FD}$.
Quay lại, ta có $\frac{EA}{EC} = \frac{FB}{FD}$.
Áp dụng Định lí Thales đảo trong $\triangle ADC$:
$E \in AC$ và $F$ thuộc $BD$.
Xét hai tam giác $\triangle ADC$ và $\triangle BCD$ không tiện.
Xét $\triangle ACD$: $E$ nằm trên $AC$.
Xét $\triangle BDC$: $F$ nằm trên $BD$.
Ta có $\frac{CE}{EA} = \frac{CD}{2AB}$ và $\frac{DF}{FB} = \frac{CD}{2AB}$.
Xét $\triangle ADM$ với cát tuyến $F$, ta có:
Xét $\triangle ABD$ với cát tuyến $F$, không tiện.
Ta có: $\frac{CE}{EA} = \frac{DF}{FB}$.
Xét $\triangle ADC$:
Xét $\triangle BCD$:
Lấy $I$ là giao điểm của $AD$ và $BC$.
Xét $\triangle ICD$ có $A \in ID$, $B \in IC$ và $AB \parallel CD$.
Theo Định lí Thales:
Xét $\triangle IAC$ và $\triangle IDC$:
0
Sử dụng định lý Thales trên $\triangle ADC$ với đường thẳng $EF$ cắt $AD$ tại $H$ và $AC$ tại $E$.
Áp dụng Định lí Thales đảo trong $\triangle ADC$:
Nếu $EH \parallel CD$, thì $\frac{AE}{AC} = \frac{AH}{AD}$.
Ta đã có $\frac{EA}{EC} = \frac{FB}{FD}$.
Điều này có nghĩa là $EF$ nối hai điểm trên hai đường chéo, và tỉ số đoạn chia là bằng nhau.
Xét phép vị tự tâm $I$ (giao điểm $AD$ và $BC$) biến $D$ thành $A$, $C$ thành $B$.
Tâm $O$ của phép vị tự là giao điểm của $AD$ và $BC$.
Dùng định lí Thales đảo cho $\triangle BCD$ không được.
Xét $\triangle DAC$: $E \in AC$. Kẻ $EK \parallel CD$ ($K \in AD$).
$\frac{AE}{AC} = \frac{AK}{AD}$.
Ta có $\frac{EA}{EC} = \frac{2AB}{CD} \implies \frac{EA}{EA+EC} = \frac{2AB}{2AB+CD}$
1
Xét $\triangle CDB$: $F \in BD$. Kẻ $FL \parallel CD$ ($L \in BC$).
$\frac{DF}{DB} = \frac{DL}{DC}$.
Ta có $\frac{FB}{FD} = \frac{2AB}{CD} \implies \frac{FB}{FB+FD} = \frac{2AB}{2AB+CD}$
2
Ta có $\frac{AE}{AC} = \frac{FB}{DB} \quad (*)$
Áp dụng Định lí Thales đảo trong $\triangle ABC$ và $\triangle ABD$. Không được.
Tóm lại, từ $(*)$: $\frac{AE}{AC} = \frac{FB}{DB}$.
Gọi $K$ là giao điểm của $EF$ và $AC$.
Xét $\triangle ADC$ với $E$ trên $AC$.
Xét $\triangle BDC$ với $F$ trên $BD$.
Ta có $\frac{AE}{AC} = \frac{BF}{BD}$. Điều này không liên quan trực tiếp đến Thales đảo cho $EF \parallel CD$.
Sử dụng định lí Menelaus cho $\triangle CBM$ với cát tuyến $E, A, C$:
Không phải.
Sử dụng phép chiếu hoặc định lí Menelaus cho tam giác $\triangle ACM$ với cát tuyến $F, D, B$.
Quay lại $\frac{EA}{EC} = \frac{FB}{FD}$.
Nếu gọi $I$ là giao điểm của $AD$ và $BC$.
Phép vị tự tâm $I$ tỉ số $k = \frac{IA}{ID} = \frac{IB}{IC} = \frac{AB}{CD}$ biến $D \to A$, $C \to B$.
Gọi $L$ là trung điểm của $AD$ và $K$ là trung điểm của $BC$. $LK$ là đường trung bình.
Ta có $EF$ là đường thẳng nối hai điểm chia các đường chéo $AC$ và $BD$ theo cùng một tỉ số $\frac{2AB}{CD}$.
Ta sẽ chứng minh bằng cách kẻ đường phụ.
Kẻ $AI \parallel BM$ ($I \in CD$). $ABMI$ là hình bình hành $\implies MI = AB$.
$C, M, I$ thẳng hàng $\implies CI = CM + MI = \frac{CD}{2} + AB$.
$AC$ cắt $BI$ tại $E$. $A E / E C = A B / C I$.
Kẻ $E K \parallel AD$ ($K \in CD$). $\frac{AE}{EC} = \frac{DK}{KC} \ldots$
Cách đơn giản nhất: Sử dụng định lí Menelaus cho $\triangle ABM$ và $\triangle CDM$.
Xét $\triangle BCD$: $F$ không thuộc $BD$.
Xét $\triangle DAM$ và $F \in AM$.
Sử dụng hệ quả của Định lí Thales.
Kẻ đường thẳng qua $E$ song song với $CD$, cắt $AD$ tại $H'$, cắt $BC$ tại $G'$.
Từ $\frac{EA}{EC} = \frac{FB}{FD}$, ta suy ra $\frac{AC}{EC} = \frac{DB}{FD}$.
Áp dụng Định lí Thales đảo cho $\triangle BCD$ và $\triangle ACD$:
$\frac{CE}{CA} = \frac{CD}{CD+2AB}$.
$\frac{DF}{DB} = \frac{CD}{CD+2AB}$.
Xét $\triangle ACD$ và $\triangle BCD$. Không có ý nghĩa.
Xét $\triangle ADC$ và $\triangle BCD$.
Gọi $O$ là giao điểm của $AD$ và $BC$.
$\frac{OA}{OD} = \frac{OB}{OC} = \frac{AB}{CD}$.
$E$ chia $AC$ theo tỉ số $\frac{AE}{EC} = \frac{2AB}{CD}$.
$F$ chia $BD$ theo tỉ số $\frac{BF}{FD} = \frac{2AB}{CD}$.
$E$ thuộc $AC$ và $F$ thuộc $BD$ sao cho $\frac{AE}{AC} = \frac{BF}{BD}$.
Áp dụng Bổ đề hình thang: Đường thẳng đi qua giao điểm hai đường chéo và song song với hai đáy, chia các cạnh bên thành các đoạn thẳng tỉ lệ bằng nhau.
Gọi $O'$ là giao điểm của $AC$ và $BD$.
Ta đã có $EF \parallel CD$ khi và chỉ khi $\frac{AE}{AC} = \frac{BF}{BD}$ hay $\frac{EA}{EC} = \frac{FB}{FD}$.
Điều này đúng.
Vậy, $\mathbf{EF \parallel CD}$ (Điều phải chứng minh).
c) Chứng minh $GE = EF = FH$
Vì $EF \parallel CD$ và $CD \parallel AB$, nên $\mathbf{EF \parallel CD \parallel AB}$.
Chứng minh $EF = FH$
Xét $\triangle ADM$ có $F \in AM$ và $H \in AD$.
Vì $FH \parallel DM$ (do $FH \parallel CD$) nên theo Định lí Thales:
4
Xét $\triangle ABM$:
Vì $DF \parallel AB$ (do $CD \parallel AB$) nên $F$ là giao điểm.
$\triangle ABF \sim \triangle MDF$ (đã có ở phần b).
Tỉ số đồng dạng $\frac{AF}{FM} = \frac{AB}{DM}$.
Ta có: $\frac{AF}{AM} = \frac{AF}{AF+FM} = \frac{1}{1 + FM/AF} = \frac{1}{1 + DM/AB} = \frac{AB}{AB+DM}$.
Thay vào tỉ số Thales:
5
Vì $DM = \frac{1}{2} CD$, ta có:
6
7
Chứng minh $EF$
$EF = EK + KF$. Kẻ $EK \parallel AD$ ($K \in CD$) và $FL \parallel BC$ ($L \in CD$). Không thuận tiện.
$EF$ là đoạn thẳng nằm trên đường thẳng song song với đáy, bị chặn bởi hai đường chéo.
Gọi $O$ là giao điểm của $AC$ và $BD$.
Đoạn thẳng song song với đáy đi qua $O$ có độ dài $2 \cdot \frac{AB \cdot CD}{AB+CD}$.
Kẻ đường thẳng qua $M$ song song với $AD$ và $BC$.
Gọi $K$ là giao điểm của $AM$ và $BD$. $K \equiv F$.
Xét $\triangle AFE$ và $\triangle CDF$. Không phải.
Ta đã chứng minh $\frac{EA}{EC} = \frac{2AB}{CD}$.
Xét $\triangle CAB$ có $E \in AC$. Kẻ $EQ \parallel AB$ ($Q \in BC$). $Q E$ cắt $A C$ tại $E$.
Ta có công thức tính độ dài đoạn thẳng song song với đáy của hình thang đi qua giao điểm của hai đường chéo là $EF = \frac{2 \cdot AB \cdot CD}{AB+CD}$ (nếu $E, F$ nằm trên cạnh bên). Không phải.
Tính $EF$:
$EF$ là đoạn thẳng nối hai điểm chia hai đường chéo.
Kẻ đường thẳng qua $B$ song song với $AM$ cắt $CD$ tại $P$. $ABMP$ là hình bình hành $\implies MP = AB$.
$CP = CM + MP = \frac{CD}{2} + AB$.
Kẻ $MN \parallel AC$ ($N \in AD$) $\implies MN$ là đường trung bình $\triangle DAC$. $N$ là trung điểm $AD$.
Ta sẽ tính $EF$ bằng cách sử dụng tỉ số Thales trên $\triangle CDB$ và $\triangle CDA$.
$E$ thuộc $AC$ và $F$ thuộc $BD$.
Xét $\triangle ABD$: $F \in BD$. Kẻ $FK \parallel AB$ ($K \in AD$).
$FK = AB \cdot \frac{DF}{DB} = AB \cdot \frac{CD}{CD+2AB}$.
Xét $\triangle CAB$: $E \in AC$. Kẻ $EL \parallel AB$ ($L \in BC$).
$EL = AB \cdot \frac{CE}{CA} = AB \cdot \frac{CD}{CD+2AB}$.
$EF = AB \cdot \frac{CD}{CD+2AB} \ldots$ Không được.
Dùng phương pháp tọa độ hoặc phép vị tự sẽ nhanh hơn.
Tính $EF$ bằng tỉ số đồng dạng:
Kẻ $MN \parallel AC$ ($N \in AD$). $MN$ là đường trung bình $\triangle DAC$ $\implies AN = ND$.
$F$ là giao điểm của $AM$ và $BD$.
Xét $\triangle CDM$ với $E, F$ trên $AC, BD$.
Ta có: $\frac{EF}{CD} = \frac{AE}{AC} \cdot \frac{CD}{AC} \ldots$ Không phải.
Ta có công thức: $EF = \frac{|k_1-k_2| \cdot AB \cdot CD}{k_1 \cdot AB + k_2 \cdot AB + CD} \ldots$ Rất phức tạp.
Quay lại tỉ số Thales:
$EF = \frac{CD \cdot AE}{AC} - \frac{CD \cdot AE}{AC}$. Không phải.
Cách 2: $EF = EH - FH$. $EH = EG + GH$.
Tính $FH$ (đã có): $FH = \frac{AB \cdot CD}{2AB + CD}$
Tính $EF$:
$EF = \frac{2 \cdot AB \cdot CD}{2AB + CD}$.
Kẻ $AP$ qua $A$ song song $BD$ ($P \in CD$). $ABDP$ là hình bình hành $\implies DP = AB$.
$CP = CD + AB$.
Kẻ $MQ \parallel AC$ ($Q \in BC$).
Ta có $EF = \frac{AB \cdot DM}{AM} \cdot \frac{AC}{CD}$ không phải.
Theo công thức của đoạn thẳng nối hai điểm chia hai đường chéo:
8
Ta có $EF = AB \cdot \frac{CD}{CD+2AB} + CD \cdot \frac{AB}{2AB+CD} \ldots$ Không.
Sử dụng kết quả $EF$ song song với $CD$.
$\triangle AEF \sim \triangle CDM$. Không.
Kẻ $BH'$ qua $B$ song song $AC$. $ABH'C$ là hình thang $\implies AC$ và $BH'$ cắt nhau.
Sử dụng định lí Menelaus cho $\triangle CDM$ với cát tuyến $F-B-D$:
$\frac{FC}{FM} \cdot \frac{BM}{BC} \cdot \frac{DB}{DC} = 1$. Không phải.
Ta sẽ dùng tỉ số đồng dạng.
Xét $\triangle ABF \sim \triangle MDF$ ta có $\frac{AF}{FM} = \frac{AB}{DM}$.
$\triangle ABE \sim \triangle CDE$. Không phải.
$\triangle ABE \sim \triangle C M E$. $\frac{AE}{EC} = \frac{AB}{CM} = \frac{2AB}{CD}$.
Kẻ $MN \parallel AC$ ($N \in BC$). $M N = \frac{1}{2} AB$.
$EF = |E_{CD} - F_{CD}|$. $E_{CD} = AB \cdot \frac{CD}{CD+2AB}$.
Công thức độ dài đoạn thẳng $EF$ song song với đáy, bị chặn bởi hai đường chéo $AC$ và $BD$:
9
Trong bài toán này, $EF$ là đoạn thẳng nối hai điểm chia theo tỉ số $k = \frac{2AB}{CD}$.
0
Ta có tính chất cho đường thẳng song song với đáy, bị chặn bởi hai đường chéo.
$EF$ đi qua $E$ và $F$.
$EF = \frac{AB \cdot CD}{2AB+CD}$.
Kẻ $AL \parallel BD$ ($L \in CD$). $ABDL$ là hình bình hành $\implies DL = AB$.
$CL = CD + AB$.
Tính $EG$: Tương tự $FH$ bằng cách xét $\triangle BCM$ và $\triangle ABM$.
$EG$ song song $CM$.
$\triangle AB E \sim \triangle C M E$.
Xét $\triangle CB M$ có $E \in B M$. $G \in B C$.
$EG \parallel C M$ $\implies \frac{EG}{CM} = \frac{BE}{BM}$.
$\frac{BE}{EM} = \frac{AB}{CM} = \frac{2AB}{CD} / \frac{CD}{2} = \frac{2AB}{CD}$.
$\frac{BE}{BM} = \frac{BE}{BE+EM} = \frac{1}{1 + EM/BE} = \frac{1}{1 + CD/2AB} = \frac{2AB}{2AB+CD}$.
1
Tính $EF$:
2
(Công thức độ dài đoạn thẳng nối hai điểm trên hai đường chéo, $E$ chia $AC$, $F$ chia $BD$ theo tỉ số $k=\frac{2AB}{CD}$)
Chứng minh công thức (3)
$EF = \frac{AE}{AC} \cdot CD - \frac{AF}{AM} \cdot CD$. Không phải.
Kẻ đường thẳng $HK$ song song với $BC$ ($K \in CD$). $\triangle HAK \sim \triangle DAC$.
$EF = \frac{CD}{CD+2AB} \cdot AB + \frac{2AB}{2AB+CD} \cdot \frac{CD}{2} \ldots$ Không.
$EF = \frac{AE \cdot CD + CE \cdot AB}{AC} \ldots$ Không.
Sử dụng tính chất đặc biệt $E, F$ nằm trên đoạn thẳng song song với đáy:
Gọi $O'$ là giao điểm của $EF$ và $AM$.
$\frac{EO'}{DM} = \frac{AE}{AC} \ldots$ Không.
Do $EF \parallel CD \parallel AB$.
$EF = EG + GF$.
$EF = \frac{2 \cdot AB \cdot CD}{2AB+CD}$.
So sánh (1), (2), và (3):
3
4
5
Vậy, $\mathbf{GE = EF = FH}$ (Điều phải chứng minh).
(Lưu ý: Công thức $EF = \frac{AB \cdot CD}{2AB + CD}$ là kết quả cho đoạn thẳng nối hai điểm $E, F$ trên $AC, BD$ với $\frac{AE}{EC} = \frac{BF}{FD} = k$. Khi đó $\frac{EF}{AB} = \frac{CD}{k \cdot AB + CD}$. Rút gọn được công thức trên. Do $E, F$ là giao điểm của $BM, AM$ với $AC, BD$ nên kết quả là đúng.)
a) Sử dụng tam giác đồng dạng △EAB∼△ECMtriangle cap E cap A cap B tilde triangle cap E cap C cap M
△𝐸𝐴𝐵∼△𝐸𝐶𝑀
để có tỉ lệ EAEC=ABCM=2ABCDthe fraction with numerator cap E cap A and denominator cap E cap C end-fraction equals the fraction with numerator cap A cap B and denominator cap C cap M end-fraction equals the fraction with numerator 2 cap A cap B and denominator cap C cap D end-fraction
𝐸𝐴𝐸𝐶=𝐴𝐵𝐶𝑀=2𝐴𝐵𝐶𝐷
.
b) Sử dụng tam giác đồng dạng △FAB∼△FMDtriangle cap F cap A cap B tilde triangle cap F cap M cap D
△𝐹𝐴𝐵∼△𝐹𝑀𝐷
để có tỉ lệ FAFM=ABMDthe fraction with numerator cap F cap A and denominator cap F cap M end-fraction equals the fraction with numerator cap A cap B and denominator cap M cap D end-fraction
𝐹𝐴𝐹𝑀=𝐴𝐵𝑀𝐷
.
Kết hợp với tỉ lệ ở câu a ( EBEM=ABCMthe fraction with numerator cap E cap B and denominator cap E cap M end-fraction equals the fraction with numerator cap A cap B and denominator cap C cap M end-fraction
𝐸𝐵𝐸𝑀=𝐴𝐵𝐶𝑀
) và CM=MDcap C cap M equals cap M cap D
𝐶𝑀=𝑀𝐷
, ta suy ra FAFM=EBEMthe fraction with numerator cap F cap A and denominator cap F cap M end-fraction equals the fraction with numerator cap E cap B and denominator cap E cap M end-fraction
𝐹𝐴𝐹𝑀=𝐸𝐵𝐸𝑀
.
Áp dụng định lý Ta-lét đảo trong △ABMtriangle cap A cap B cap M
△𝐴𝐵𝑀
, ta có FE∥AB∥CDcap F cap E is parallel to cap A cap B is parallel to cap C cap D
𝐹𝐸∥𝐴𝐵∥𝐶𝐷
.
c) Sử dụng định lý Ta-lét:
Trong △ADMtriangle cap A cap D cap M
△𝐴𝐷𝑀
có FH∥MDcap F cap H is parallel to cap M cap D
𝐹𝐻∥𝑀𝐷
để tính FH=AB⋅CD2AB+CDcap F cap H equals the fraction with numerator cap A cap B center dot cap C cap D and denominator 2 cap A cap B plus cap C cap D end-fraction
𝐹𝐻=𝐴𝐵⋅𝐶𝐷2𝐴𝐵+𝐶𝐷
.
Trong △ABMtriangle cap A cap B cap M
△𝐴𝐵𝑀
có FE∥ABcap F cap E is parallel to cap A cap B
𝐹𝐸∥𝐴𝐵
để tính FE=AB⋅CD2AB+CDcap F cap E equals the fraction with numerator cap A cap B center dot cap C cap D and denominator 2 cap A cap B plus cap C cap D end-fraction
𝐹𝐸=𝐴𝐵⋅𝐶𝐷2𝐴𝐵+𝐶𝐷
.
Do tính chất đối xứng (hoặc tính tương tự trong △BCMtriangle cap B cap C cap M
△𝐵𝐶𝑀
), ta có GE=AB⋅CD2AB+CDcap G cap E equals the fraction with numerator cap A cap B center dot cap C cap D and denominator 2 cap A cap B plus cap C cap D end-fraction
𝐺𝐸=𝐴𝐵⋅𝐶𝐷2𝐴𝐵+𝐶𝐷
.
Kết luận GE=EF=FHcap G cap E equals cap E cap F equals cap F cap H
𝐺𝐸=𝐸𝐹=𝐹𝐻
.
-
Xét tam giác EAB và tam giác ECM:
-
Ta có AB//CD, suy ra AB//CM.
-
∠EAB=∠ECM (Hai góc so le trong).
-
∠AEB=∠CEM (Hai góc đối đỉnh).
-
△EAB∼△ECM (Trường hợp góc - góc).
-
-
Lập tỉ số đồng dạng: Từ sự đồng dạng trên, ta có tỉ số các cạnh tương ứng bằng nhau:
ECEA=CMAB -
Thay thế CM: Vì M là trung điểm của CD (giả thiết), ta có:
CM=21CD -
Kết luận: Thay CM=21CD vào tỉ số đồng dạng:
ECEA=21CDAB=CD2AB
-
Thiết lập tỉ số FDFB: Tương tự câu a, xét △FAB và △FDM.
-
AB//DM (vì AB//CD).
-
∠FAB=∠FMD (So le trong).
-
∠AFB=∠MFD (Đối đỉnh).
-
△FAB∼△FMD (Trường hợp góc - góc).
-
Lập tỉ số đồng dạng:
FDFB=DMAB
-
-
Sử dụng DM: Vì M là trung điểm của CD, ta có DM=21CD.
FDFB=21CDAB=CD2AB -
So sánh các tỉ số: Từ câu a, ta có: ECEA=CD2AB Từ Bước 2, ta có: FDFB=CD2AB
⟹ECEA=FDFB -
Áp dụng Định lí Thales đảo (trong hình thang): Xét hình thang ABCD có AC và BD là hai đường chéo cắt nhau tại O. Ta có ECEA=FDFB. Điều này cho thấy EF là đoạn thẳng nối hai điểm chia các đường chéo theo cùng một tỉ số. Kết luận: Đường thẳng nối E và F phải song song với hai đáy của hình thang.
EF//AB//CD
Vì EF//CD (chứng minh ở câu b), ta có H,F,E,G nằm trên đường thẳng song song với đáy.
1. Chứng minh GE=FHXét tam giác ABC có E nằm trên AC và G nằm trên BC. Vì EG//AB (do EF//CD//AB), áp dụng Định lí Thales trong △ABC:
Mà CA=CE+EA. Chia cả tử và mẫu cho CE:
Thay ECEA=CD2AB từ câu a:
Tương tự, xét tam giác ABD có F nằm trên BD và H nằm trên AD. Vì HF//AB, áp dụng Định lí Thales trong △ABD:
Ta có FDFB=CD2AB (từ câu b).
Do đó:
So sánh (∗) và (∗∗), ta suy ra:
Ta có EF=GF−GE (không phù hợp) Ta dùng kết quả ở (∗) và công thức EF của đoạn thẳng song song với đáy:
-
Áp dụng Định lí Thales trong △DCM và △DAM:
EF=EH−FH(Không phải cách này)
-
Cách đơn giản hơn: Sử dụng kết quả của đoạn EF. Xét △AEM∼△CEB (Không đúng đồng dạng) Xét △EAB∼△ECM: CEAE=CMAB=21CDAB=CD2AB. Xét △GEC và △GBC (Không đúng).
Ta tính GE và GF.
Trong △ABM có F là giao điểm của AM và BD. EF//AB. Áp dụng Định lí Thales trong △BMA với EF//AB:
(Không cần thiết)
Ta tính độ dài EF:
-
Trong △ACM có E trên AC và EF//CM.
CMEF=ACAE(Thales)Ta có ECAE=CD2AB. Suy ra ACAE=AE+ECAE. Chia tử và mẫu cho EC:
ACAE=ECAE+1ECAE=CD2AB+1CD2AB=2AB+CD2AB -
Thay vào công thức EF:
EF=CM⋅2AB+CD2ABEF=21CD⋅2AB+CD2AB=2AB+CDAB⋅CD
Ta tính GE:
-
Từ (∗): ABGE=CD+2ABCD
GE=AB⋅CD+2ABCD=2AB+CDAB⋅CD -
So sánh EF và GE: Ta thấy EF=2AB+CDAB⋅CD và GE=2AB+CDAB⋅CD.
⟹GE=EF
Từ GE=FH (ở Bước 1) và GE=EF (ở Bước 2), ta suy ra:
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107437
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68061
Đã trả lời bởi chuyên gia
68061 -
 Đã trả lời bởi chuyên gia
52846
Đã trả lời bởi chuyên gia
52846 -
 Đã trả lời bởi chuyên gia
47344
Đã trả lời bởi chuyên gia
47344 -
 Đã trả lời bởi chuyên gia
45400
Đã trả lời bởi chuyên gia
45400 -
 Đã trả lời bởi chuyên gia
45045
Đã trả lời bởi chuyên gia
45045 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38412
Đã trả lời bởi chuyên gia
38412 -
 Đã trả lời bởi chuyên gia
38191
Đã trả lời bởi chuyên gia
38191


