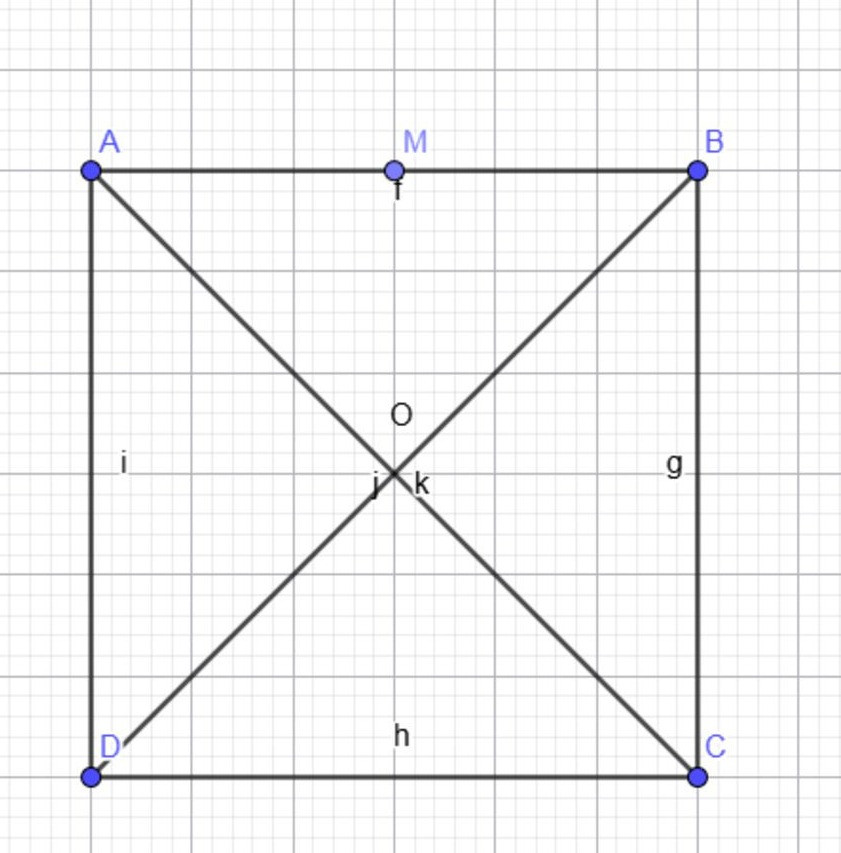
Cho hình vuông ABCD, tâm OM là trung điểm của AB tính | vectơ AB | và | vectơ OA + vectơ OB |
$\Huge\color{white}{\text{.}}$
· 3 tuần trước
? vecto AB theo cái gì ms dc chứ
$\Huge\color{white}{\text{.}}$
· 3 tuần trước
à hiểu rồi
Quảng cáo
2 câu trả lời 107
Ta có :
`|vec(AB)| =AB` (vì là hình vuông)
O là tâm của hình vuông
`->OA = OB`
`->\hat(AOB )= 90^0`
Lại có : `AC = AB\sqrt(2)`
`->OA = (AC)/2 = (AB)/\sqrt(2) `
`(|vec(OA) + vec(OB)|)^2`
`= OA^2 + OB^2`
`= 2OA^2`
`->|vec(OA) + vec(OB)| = OA\sqrt(2)= (AB)/(\sqrt(2)).\sqrt(2) = AB`
Kết quả ngắn gọn:
Đặt tâm O của hình vuông tại gốc tọa độ, AB nằm phía trên. Khi đó:
(|\vec{AB}| = a) (a là độ dài cạnh hình vuông)
(|\vec{OA} + \vec{OB}| = a)
⇒ Hai độ lớn đều bằng cạnh hình vuông.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
89037
Đã trả lời bởi chuyên gia
89037 -
 Đã trả lời bởi chuyên gia
59731
Đã trả lời bởi chuyên gia
59731 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
58851
Đã trả lời bởi chuyên gia
58851 -
 Đã trả lời bởi chuyên gia
50834
Đã trả lời bởi chuyên gia
50834 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
48266
Đã trả lời bởi chuyên gia
48266 -
 Đã trả lời bởi chuyên gia
38581
Đã trả lời bởi chuyên gia
38581
Gửi báo cáo thành công!


