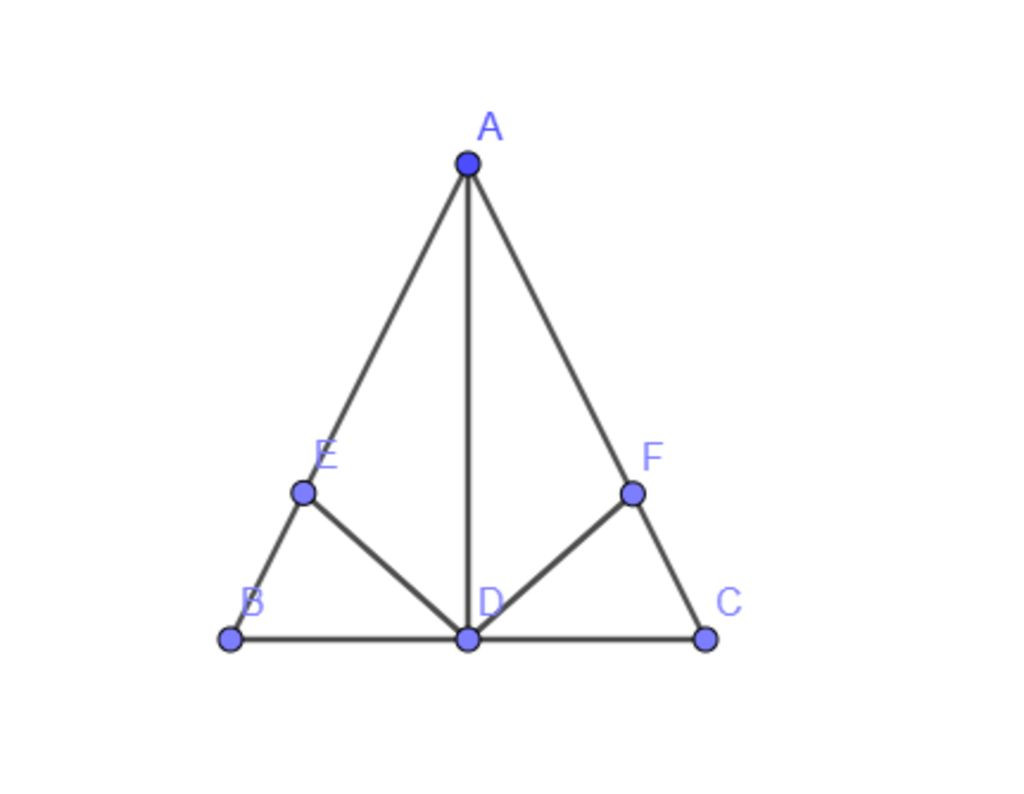
Cho tam giác ABC có AB = AC tia phân giác góc A cắt BC tại D
a, chứng minh rằng D là trung điểm của BC và AD vuông góc với BC
b, lấy E thuộc AB ,f thuộc AC, BE = CF chứng minh rằng DA là tia phân giác của EDF .
Mọi người vẽ hình giúp mình với ạ
a, chứng minh rằng D là trung điểm của BC và AD vuông góc với BC
b, lấy E thuộc AB ,f thuộc AC, BE = CF chứng minh rằng DA là tia phân giác của EDF .
Mọi người vẽ hình giúp mình với ạ
Quảng cáo
1 câu trả lời 79
`a)`
Có `AB=AC => \triangleABC` cân tại `A`
mà `AD` là đường phân giác
`=> AD` cũng là đường cao, đường trung tuyến
hay `D` là trung điểm của `BC, AD\botBC`
`b)`
Có `AB=AE+EB; AC=AF+FC`
mà `AB=AC; BE=CF`
`=> AE=AF`
Xét `triangleAED` và `\triangleAFD` có:
`AE=AF (cmt)`
`\hat{EAD}=\hat{FAD} (AD là phân giác)`
`AD` chung
Vậy `\triangleAED=\triangleAFD (c.g.c)`
`=> \hat{ADE}=\hat{ADF}` (2 góc tương ứng)
hay `DA là phân giác của \hat{EDF}`
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120962
-
 Đã trả lời bởi chuyên gia
81713
Đã trả lời bởi chuyên gia
81713 -
 Đã trả lời bởi chuyên gia
59651
Đã trả lời bởi chuyên gia
59651 -
 Đã trả lời bởi chuyên gia
39669
Đã trả lời bởi chuyên gia
39669
Gửi báo cáo thành công!


