Bài 1 Cho hình thang ABCD lấy M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD, DA
a) Chứng minh MN song song AC
b) tứ giác MNPQ là hình gì ?
Bài 2 Cho tam giác ABC có hai đường trung tuyến BM ,CN cắt nhau tại g Gọi i ,k lần lượt là trung điểm của GB, GC
a) Chứng minh MN = IK
b) tứ giác mnik là hình gì ?
Quảng cáo
3 câu trả lời 389
Bài 1:
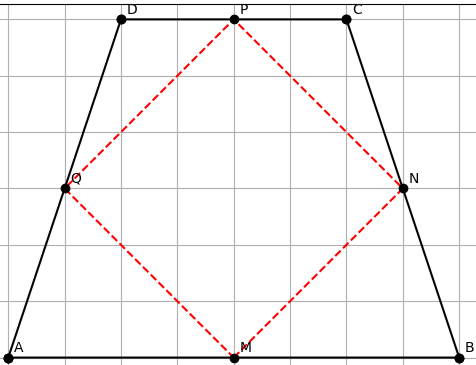
a) Chứng minh MN // AC
- Xét tam giác ABC, M là trung điểm AB, N là trung điểm BC.
- Theo định lý đường trung bình của tam giác: Đường nối hai trung điểm của hai cạnh bất kỳ song song với cạnh thứ ba.
- Trong tam giác ABC, MN nối trung điểm M và N → song song với AC.
=> MN // AC
b) Tứ giác MNPQ là hình gì?
- Xét các tam giác và các đoạn nối trung điểm:
Trong tam giác BCD, NP nối trung điểm BC và CD → song song với BD.
Trong tam giác ABD, MQ nối trung điểm AB và AD → song song với BD.
Trong tam giác ADC, QPnối trung điểm DA và DC → song song với AC.
Nhận xét: Tứ giác MNPQ có hai cặp cạnh đối song song:
MN // QP và MQ // NP
=> Tứ giác MNPQ là hình bình hành.
Bài 2: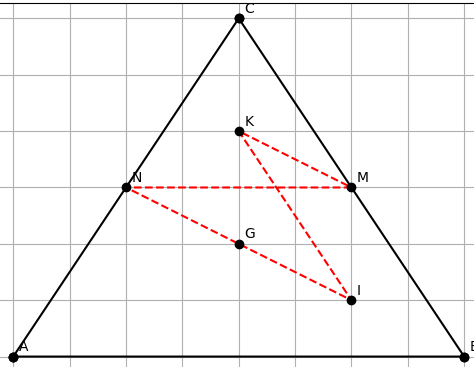
a) Chứng minh MN = IK
- G là trọng tâm tam giác ABC. Theo tính chất trọng tâm:
AG : GM = BG : GN = CG : GP = 2 : 1
- Lấy I là trung điểm GB, K là trung điểm GC.
- Xét tam giác BGC: đường nối hai trung điểm I và K song song với BC và bằng nửa BC.
Đồng thời, MN cũng nối trung điểm hai cạnh của tam giác có BC là cạnh → MN = IK.
b) Tứ giác MNIK là hình gì?
- Xét tứ giác MNIK:
MN song song và bằng IK (theo định lý đường trung bình tam giác).
MI song song với NK (do đều nối trung điểm các cạnh).
Nhận xét: Tứ giác MNIK có hai cặp cạnh đối song song và bằng nhau → tứ giác MNIK là hình bình hành.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107437
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68061
Đã trả lời bởi chuyên gia
68061 -
 Đã trả lời bởi chuyên gia
52846
Đã trả lời bởi chuyên gia
52846 -
 Đã trả lời bởi chuyên gia
47344
Đã trả lời bởi chuyên gia
47344 -
 Đã trả lời bởi chuyên gia
45400
Đã trả lời bởi chuyên gia
45400 -
 Đã trả lời bởi chuyên gia
45045
Đã trả lời bởi chuyên gia
45045 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38412
Đã trả lời bởi chuyên gia
38412 -
 Đã trả lời bởi chuyên gia
38191
Đã trả lời bởi chuyên gia
38191



