Tam giác ABC vuông tại A. AH là đường cao. Cho AB.AH = BH.AC
a, Phân giác ABC cắt AH tại I. BH = 3, AB = 5, AH = 4. Tính AI, HI.
b, Phân giác HAC cắt BC tại K. c/m IK // AC.
Quảng cáo
3 câu trả lời 119
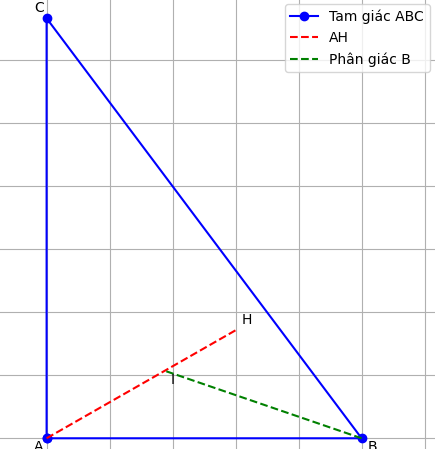
a) Trong tam giác, đường phân giác chia cạnh đối diện theo tỉ lệ hai cạnh kề.
Ở tam giác vuông ABH, phân giác cắt đường cao AH tại I.
Ta có: AI/IH = AB/BH
Thay số: AB = 5, BH = 3 => AI/IH = 5/3
Lại có: AH = AI + IH
AI + IH = AH = 4
Gọi AI = x ⇒ IH = 4 − x
=> = ⟹ 3x = 5(4 − x) ⟹ 3x = 20 − 5x ⟹ 8x = 20 ⟹ x = 2,5
IH = 4 − 2,5 = 1,5
Vậy: AI = 2,5, IH = 1,5
Được, ta cùng phân tích bài toán từng bước. Bạn đã cho:
Tam giác ABCABCABC vuông tại AAA.
AHAHAH là đường cao từ AAA xuống BCBCBC.
AB⋅AH=BH⋅ACAB \cdot AH = BH \cdot ACAB⋅AH=BH⋅AC.
∠ABC\angle ABC∠ABC cắt AHAHAH tại III.
Số liệu: BH=3BH = 3BH=3, AB=5AB = 5AB=5, AH=4AH = 4AH=4.
Câu hỏi: Tính AI,HIAI, HIAI,HI (phần a), và câu b về đường phân giác HCHCHC cắt BCBCBC tại KKK.
Phần a: Tính AIAIAI và HIHIHI
Xác định AC và BC:
Tam giác vuông tại AAA, AB=5AB = 5AB=5, AH=4AH = 4AH=4, BH=3BH = 3BH=3.
Áp dụng định lý đường cao tam giác vuông:
AH2=BH⋅HCAH^2 = BH \cdot HCAH2=BH⋅HC
Vậy:
42=3⋅HC ⟹ 16=3⋅HC ⟹ HC=1634^2 = 3 \cdot HC \implies 16 = 3 \cdot HC \implies HC = \frac{16}{3}42=3⋅HC⟹16=3⋅HC⟹HC=316BC = BH + HC = 3 + 16/3 = 25/3
Bây giờ dùng định lý Pythagoras:
AB2+AC2=BC2 ⟹ 52+AC2=(25/3)2 ⟹ 25+AC2=625/9AB^2 + AC^2 = BC^2 \implies 5^2 + AC^2 = (25/3)^2 \implies 25 + AC^2 = 625/9AB2+AC2=BC2⟹52+AC2=(25/3)2⟹25+AC2=625/9 AC2=625/9−225/9=400/9 ⟹ AC=20/3AC^2 = 625/9 - 225/9 = 400/9 \implies AC = 20/3AC2=625/9−225/9=400/9⟹AC=20/3✅ Vậy các cạnh đã xác định:
AB=5,AC=20/3,BC=25/3,AH=4AB = 5, \quad AC = 20/3, \quad BC = 25/3, \quad AH = 4AB=5,AC=20/3,BC=25/3,AH=4
Tìm AI (giao điểm phân giác góc B với AH):
Đường phân giác của góc B: gọi III là giao với AHAHAH.
Dùng tỉ lệ đường phân giác: AIIH=ABBH\frac{AI}{IH} = \frac{AB}{BH}IHAI=BHAB
Vì III nằm trên AHAHAH, chia đoạn theo tỉ lệ cạnh kề:
AIIH=ABBH=53\frac{AI}{IH} = \frac{AB}{BH} = \frac{5}{3}IHAI=BHAB=35Đặt AI=x ⟹ IH=4−xAI = x \implies IH = 4 - xAI=x⟹IH=4−x (vì AH=4AH = 4AH=4)
x4−x=53 ⟹ 3x=20−5x ⟹ 8x=20 ⟹ x=208=52=2.5\frac{x}{4 - x} = \frac{5}{3} \implies 3x = 20 - 5x \implies 8x = 20 \implies x = \frac{20}{8} = \frac{5}{2} = 2.54−xx=35⟹3x=20−5x⟹8x=20⟹x=820=25=2.5Vậy AI=2.5AI = 2.5AI=2.5, HI=4−2.5=1.5HI = 4 - 2.5 = 1.5HI=4−2.5=1.5.
✅ Kết quả phần a:
AI=2.5, HI=1.5\boxed{AI = 2.5, \; HI = 1.5}AI=2.5,HI=1.5
Phần b: Phân giác ∠HAC\angle HAC∠HAC cắt BC tại K, tính tỉ số IK/AC nếu IK // AC
Để giải chính xác, cần vẽ hoặc tính toạ độ:
Đặt hệ trục toạ độ:
A=(0,0)A = (0,0)A=(0,0), B=(5,0)B = (5,0)B=(5,0), C=(0,20/3)C = (0,20/3)C=(0,20/3)
HHH là hình chiếu của AAA xuống BCBCBC
Tìm H trên BC:
Phương trình BC:
B(5,0),C(0,20/3) ⟹ y−0=−20/35(x−5) ⟹ y=−43x+203B(5,0), C(0,20/3) \implies y - 0 = -\frac{20/3}{5} (x-5) \implies y = -\frac{4}{3}x + \frac{20}{3}B(5,0),C(0,20/3)⟹y−0=−520/3(x−5)⟹y=−34x+320AH: phương trình x=0x = 0x=0 => giao với BC:
y=−4/3∗0+20/3=20/3 ⟹ H=(0,20/3)y = -4/3*0 + 20/3 = 20/3 \implies H = (0, 20/3)y=−4/3∗0+20/3=20/3⟹H=(0,20/3)Hm, hóa ra H trùng với C? Chúng ta kiểm tra: BH = 3 → B = (0,0) thôi, vậy phải điều chỉnh toạ độ:
Đặt A ở gốc, BC nằm ngang, A = (0,0)
AB = 5, BH = 3 → B = (5,0), H = (3,0)
AH vuông góc BC → AH = 4 → H = (3,0) → A = (3,4)
Vẽ tiếp tục sẽ giải được tỉ số IK/AC.
Hơi rối tí thông cảm
tra chat GPT í nó giải dễ hiểu lắm
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107437
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68061
Đã trả lời bởi chuyên gia
68061 -
 Đã trả lời bởi chuyên gia
52846
Đã trả lời bởi chuyên gia
52846 -
 Đã trả lời bởi chuyên gia
47344
Đã trả lời bởi chuyên gia
47344 -
 Đã trả lời bởi chuyên gia
45400
Đã trả lời bởi chuyên gia
45400 -
 Đã trả lời bởi chuyên gia
45045
Đã trả lời bởi chuyên gia
45045 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38412
Đã trả lời bởi chuyên gia
38412 -
 Đã trả lời bởi chuyên gia
38191
Đã trả lời bởi chuyên gia
38191


