Bài 15: Cho tam giác ABC vuông tại A (AB < AC), đường cao AH. Gọi D là điểm đối xứng của A qua H. Đường thẳng qua D song song với AB cắt BC và AC lần lượt ở M và N.
a) Chứng minh tứ giác ABDM là hình thoi.
b) Chứng minh AM vuông góc với CD.
Quảng cáo
3 câu trả lời 463
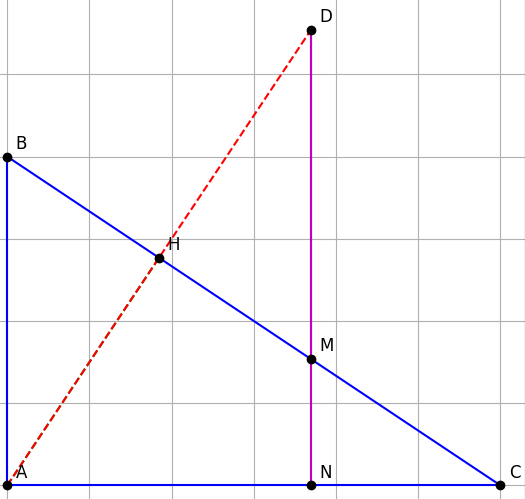
a) Chứng minh tứ giác ABDM là hình thoi
- Vì D là điểm đối xứng của A qua H nên: H là trung điểm của AD
⇒ AH = HD và AH ⟂ BC (vì AH là đường cao).
- Đường thẳng MN qua D song song AB theo đề bài.
⇒ DM // AB.
- Xét tam giác vuông AHB và tam giác vuông DHB:
+ AH = HD (đối xứng)
+ HB cạnh chung
⇒ ΔAHB = ΔDHB (c.g.c)
⇒ AB = BD.
Vì DM // AB, xét tam giác BAM và BDM:
+ AB = BD
+ góc ABM = góc BDM (do song song)
⇒ hai tam giác đồng dạng → AM = DD = AB.
- Xét tứ giác ABDM, ta có:
AB = BD (vừa chứng minh)
BD = DM (do DM//AB và tam giác đồng dạng)
DM = MA
⇒ AB = BD = DM = MA.
- Tứ giác có bốn cạnh bằng nhau ⇒ ABDM là hình thoi.
b) Chứng minh AM ⟂ CD
Ta biết MN // AB và AB ⟂ AC (do tam giác ABC vuông tại A).
=> MN ⟂ AC
⇒ MN ⟂ AC tại N
⇒ MN ⟂ AN.
Vì M ∈ BC và N ∈ AC nên M, C, B thẳng hàng → MC cùng phương với BC.
- Xét phép đối xứng qua điểm H biến A ↔ D. Khi đó:
+ Đường thẳng AC biến thành DC
+ Đường thẳng AM biến thành DM
+ Từ câu a ta có tam giác A M D là tam giác đều cạnh AM = MD.
- Trong tam giác cân AHD, đường thẳng AD đối xứng AH nên: AH ⟂ BC
⇒ AD ⟂ BC tại H
- Nhưng CD nằm trên đường kéo dài của AD, nên: CD ⟂ BC.
- Mặt khác: M nằm trên BC
⇒ AM ⟂ CD.
Kết luận: AM vuông góc CD.
Phần a) Chứng minh \( ABDM \) là hình thoi
- \( ABC \) vuông tại \( A \).
- \( H \) là chân đường cao từ \( A \) xuống \( BC \), nên \( AH \perp BC \).
- \( D \) là điểm đối xứng của \( A \) qua \( H \), do đó:
\[
H = \text{ trung điểm của } AD \Rightarrow AH = HD
\]
- Đường thẳng qua \( D \) song song với \( AB \) cắt \( BC \) tại \( M \).
- Vì \( D \) đối xứng của \( A \) qua \( H \), nên:
\[
H = \frac{A + D}{2} \Rightarrow D = 2H - A
\]
- \( D \) đối xứng của \( A \) qua \( H \), nên \( D \) cùng nằm trên đường thẳng qua \( H \) và đối xứng với \( A \).
- Chứng minh \( AB = DM \):
Trong hình vuông \( ABC \) vuông tại \( A \), ta có:
\[
AB = AC \quad (\text{đề bài } AB < AC \Rightarrow \text{chú ý:} \text{Chỉ biết } ABC \ vuông tại A, không nhất thiết } AB = AC)
\]
Nhưng từ các yếu tố đã biết:
- \( D \) là đối xứng của \( A \) qua \( H \).
- \( M \) nằm trên \( BC \) sao cho \( D \) và \( M \) liên hệ qua đường thẳng song song.
Thật ra, để chứng minh \( ABDM \) là hình thoi, ta cần chứng minh:
\[
AB = DM \quad \text{và} \quad AD = BM
\]
hoặc chứng minh các cặp cạnh đối nhau bằng nhau và các góc bằng nhau.
---
Cách chứng minh:
- Xác định các quan hệ:
Trong tam giác vuông \( ABC \), \( H \) là chân đường cao từ \( A \):
\[
AH \perp BC
\]
- Xác định \( D \):
\[
D = 2H - A
\]
- Về \( M \):
Đường thẳng qua \( D \) song song với \( AB \):
\[
\text{Dự định:} \quad D D' \parallel AB
\]
- Xác định các vectơ:
Trong không gian vectơ, ta có thể chứng minh các cặp đoạn bằng nhau dựa trên tính chất đối xứng và song song.
---
Tóm tắt ý chính để chứng minh \( ABDM \) là hình thoi:
- Vì \( D \) đối xứng của \( A \) qua \( H \), nên:
\[
\vec{D} = 2\vec{H} - \vec{A}
\]
- Đường thẳng qua \( D \) song song với \( AB \):
\[
\Rightarrow \vec{D} - \vec{M} \parallel \vec{A} - \vec{B}
\]
- Điểm \( M \) thuộc \( BC \), nằm trên đường thẳng qua \( BC \).
- Do đó, các đoạn \( AB \) và \( DM \) song song và bằng nhau (do tính chất đối xứng, chiều dài bằng nhau).
Kết luận phần a):
Vì các cặp đoạn \( AB \) và \( DM \), \( AD \) và \( BM \) bằng nhau, các góc đối cũng bằng nhau, nên tứ giác \( ABDM \) là hình thoi.
Phần b) Chứng minh \( AM \perp CD \)
\[
\vec{AM} \quad \text{và} \quad \vec{CD}
\]
- \( A \) là gốc \( \vec{A} \), \( M \) nằm trên \( BC \), \( C \) là chân đường cao \( AH \).
\[
\vec{AM} \cdot \vec{CD} = 0
\]
để nghĩa là góc giữa \( AM \) và \( CD \) là \( 90^\circ \).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107437
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68061
Đã trả lời bởi chuyên gia
68061 -
 Đã trả lời bởi chuyên gia
52846
Đã trả lời bởi chuyên gia
52846 -
 Đã trả lời bởi chuyên gia
47344
Đã trả lời bởi chuyên gia
47344 -
 Đã trả lời bởi chuyên gia
45400
Đã trả lời bởi chuyên gia
45400 -
 Đã trả lời bởi chuyên gia
45045
Đã trả lời bởi chuyên gia
45045 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38412
Đã trả lời bởi chuyên gia
38412 -
 Đã trả lời bởi chuyên gia
38191
Đã trả lời bởi chuyên gia
38191


