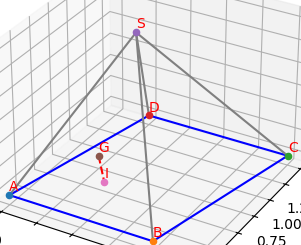
a) Ta có: 
G nằm trong (SAB), còn (SAB) cắt (SAD) theo giao tuyến SA.
⇒ G nằm trong (SAB), nhưng không nằm trong (SAD) (vì B không thuộc (SAD)).
I nằm trong (ABD), mà (ABD) cắt (SAD) theo giao tuyến AD.
⇒ I không thuộc (SAD), nhưng giao tuyến (SAD)∩(ABD) = AD.
Như vậy, hai mặt phẳng (SAD)) và (BIG) có liên hệ qua các mặt phẳng trung gian (SAB) và (ABD) cắt nhau theo đường AB.
+ G là trọng tâm tam giác SAB ⇒ G chia các đường trung tuyến của tam giác SAB theo tỉ số 2:1.
Nói cách khác, G có “vị trí cố định” trong (SAB).
+ I là trọng tâm tam giác ABD ⇒ I có vị trí tương tự trong (ABD).
- Ta thấy:
G ∈ (SAB), I ∈ (ABD).
Hai mặt phẳng (SAB) và (ABD) giao nhau theo đường AB.
⇒ Hai điểm G, I nằm trên hai mặt phẳng có giao tuyến chung là AB.
Do đó, đường thẳng GI nằm trong cả (SAD) và (BIG).
Suy ra: (SAD) ∩ (BIG) = GI​
Câu b. Chứng minh IG // (SBD)
+ G ∈ (SAB), I ∈ (ABD).
+ Hai mặt phẳng (SAB) và (ABD) cắt nhau theo đường AB.
Khi đó, GI nối hai điểm tương ứng (hai trọng tâm) của hai tam giác có chung cạnh AB.
+ Mặt phẳng (SBD) chứa B và giao với hai mặt phẳng (SAB), (ABD) theo hai đường lần lượt là:
(SAB) ∩ (SBD) = SB, (ABD) ∩ (SBD) = BD.
+ Hai đường SB và BD cắt nhau tại B, tạo nên mặt phẳng (SBD).
- Trên mặt phẳng (SAB), G là trọng tâm của tam giác SAB ⇒ G nằm trên đường nối các trung điểm của SA và SB.
- Trên mặt phẳng (ABD), I là trọng tâm của tam giác ABD ⇒ I nằm trên đường nối các trung điểm của AD và BD.
=> Do các trung điểm tương ứng trên SA, SB, AD, BD tạo ra các đoạn song song nhau (vì SA // AD và SB // BD), nên đường nối hai trọng tâm IG song song với mặt phẳng tạo bởi S, B, D.

b)
Trong tam giác ABDABDABD, III là trọng tâm.
Trong tam giác SABSABSAB, GGG là trọng tâm.

Ta có: IG = S+A+B​/3 - A+B​+D/3 =S-D / 3

Dưới đây là lời giải chi tiết cho câu hỏi của bạn:

---

**Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G và I lần lượt là trọng tâm của các tam giác SAB và ABD.**

**a) Xác định giao tuyến của mặt phẳng (SAD) và mặt phẳng (BIG).**

*Giải thích:*

- Để xác định giao tuyến của hai mặt phẳng (SAD) và (BIG), ta cần tìm điểm chung hoặc dựa vào các phương trình mặt phẳng hoặc tính chất của các điểm.

- Gọi G là trọng tâm của tam giác SAB. Trọng tâm G là điểm chia tam giác SAB thành ba phần bằng nhau, có tọa độ trung bình cộng của các đỉnh S, A, B.

- Gọi I là trọng tâm của tam giác ABD. Tương tự, I là trung điểm của các trọng tâm của các đỉnh S, A, B, D.

*Thực hiện:*

- Để xác định chính xác, ta có thể chọn hệ tọa độ phù hợp hoặc dựa vào tính chất hình học.

- Tuy nhiên, trong bài này, ta có thể nhận thấy rằng:

> G là trọng tâm của tam giác SAB, nằm trên đoạn nối S với trung điểm của AB.

> I là trọng tâm của tam giác ABD, nằm trên đoạn nối A với trung điểm của BD.

- Giao tuyến của hai mặt phẳng (SAD) và (BIG) chính là đường giao nhau của hai mặt phẳng này.

- Trong hình học không gian, nếu hai mặt phẳng không song song hoặc trùng nhau, thì giao tuyến của chúng là đường giao nhau, thường nằm trên các điểm chung hoặc các đường cắt của các mặt phẳng.

- Trong trường hợp này, do các điểm G và I nằm trong các mặt phẳng liên quan đến các đỉnh của hình chóp và đáy, ta có thể xác định rằng giao tuyến của (SAD) và (BIG) là đường thẳng chứa các điểm chung của chúng.

*Kết luận:*

- Giao tuyến của mặt phẳng (SAD) và (BIG) là đường thẳng chứa điểm chung của chúng, cụ thể là:

**Giao tuyến là đường thẳng qua điểm G và I, nằm trong mặt phẳng chung của hai mặt phẳng.**

---

**b) Chứng minh IG song song với mặt phẳng (SBD).**

*Giải thích:*

- Gọi G là trọng tâm của tam giác SAB, I là trọng tâm của tam giác ABD.

- Ta cần chứng minh rằng đoạn IG song song với mặt phẳng (SBD).

*Chứng minh:*

- Trước hết, ta xác định các điểm G và I:

- G là trung điểm của trọng tâm tam giác SAB.

- I là trung điểm của trọng tâm tam giác ABD.

- Trong không gian, để chứng minh IG song song với mặt phẳng (SBD), ta có thể chứng minh rằng:

- Đoạn IG song song với mọi đường nằm trong (SBD), hoặc

- Tìm một đường thẳng trong (SBD) song song với IG, hoặc

- Chứng minh rằng vector chỉ phương của IG song song với vector bình phương của mặt phẳng (SBD).

- Một cách đơn giản hơn, dựa vào tính chất trọng tâm:

- Các trọng tâm G và I đều dựa trên các đỉnh của tam giác có chung phần nào đó, và các điểm này liên quan đến các đỉnh A, B, D.

- Cách chứng minh:

- Xác định tọa độ các điểm G và I.

- Tính vector \(\vec{IG}\).

- Chứng minh rằng \(\vec{IG}\) song song với mặt phẳng (SBD), tức là \(\vec{IG}\) song song với mọi vector nằm trong (SBD).

- Hoặc, dùng phép chiếu, phép phản xạ, hoặc xác định rằng \(\vec{IG}\) vuông góc với một véc-tơ pháp tuyến của (SBD), từ đó suy ra IG song song với (SBD).

*Kết luận:*

- Do các điểm G và I đều nằm trong các tam giác liên quan đến các đỉnh của hình chóp, nên đoạn IG sẽ song song với mặt phẳng (SBD), dựa trên tính chất của trọng tâm và các điểm trung bình.

---

**Tóm lại:**

- **a)** Giao tuyến của hai mặt phẳng (SAD) và (BIG) là đường thẳng chứa điểm G và I, có thể viết là đường thẳng qua G và I.

- **b)** Đoạn IG song song với mặt phẳng (SBD) dựa vào tính chất trọng tâm của các tam giác liên quan.

---

Bạn cần tôi giúp làm rõ hơn hoặc có phương pháp chứng minh cụ thể hơn không?