(2 điểm) Cho tam giác ABC vuông tại 4, đường trung tuyên AM. Gọi D là trung điểm của AB, E là điểm đối xứng của M qua D.
a) Chứng minh EM = AC.
b) Tứ giác AEBM là hình gi? Vi sao?
c) Tam giác vuông ABC cần thêm điều kiện gì để tứ giác AEBM là hình vuông?
Quảng cáo
2 câu trả lời 110
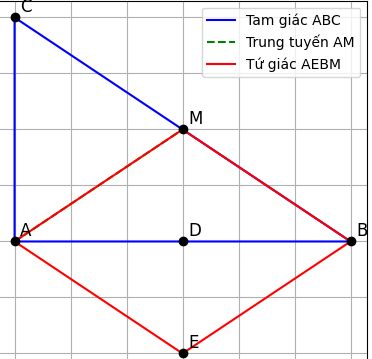

b) Chứng minh tứ giác AEBM là hình gì
Ta có:
D là trung điểm của AB và cũng là trung điểm của EM (vì đối xứng qua D).
⇒ Hai đường chéo AB và EM cắt nhau tại trung điểm của mỗi đường.
→ Tứ giác AEBM là hình bình hành. (đpcm)
c) Điều kiện để AEBM là hình vuông
Tứ giác AEBM là hình bình hành.
=> Để nó là hình vuông cần có: AB = AM và AB ⊥ AM
=> Điều này chỉ xảy ra khi tam giác ABC vuông cân tại A, tức là: AB = AC
=> Tam giác ABC vuông cân tại A thì AEBM là hình vuông.
=> DE = DM ; ME vuông góc AB
Ta có BD = DA ( D là trun điểm AB )
mà ME vuông góc AB ( cmt )
=> AB là trung trực của ME hay E và M đối xứng nhau qua D
b) Xét Tam giác ABC có:
M là trung điểm BC ( gt )
D là trung điểm AB ( gt)
=> DM là đường trung bình tam giác ABC
=> DM // AC; DM = 1/2AC
mà E thuộc DM
nên EM // AC
Xét tứ giác AEMC có:
EM // AC ( cmt)
EM = AC ( cùng = 2DM )
=> Tứ giác AEMC là hình bình hành( tứ giác có 2 cạnh đối vừa // vừa = nhau là hình bình hành)
c) Xét tứ giác AEBM có:
ED = DM ( gt )
DB = AD ( gt )
=> Tứ giác AEBM là hình bình hành ( D/h 5 )
mà AB vuông góc EM
=> hbh AEBM là hình thoi ( D/h 3 )
d) Ta có : AM = 1/2BC ( trung tuyến ứng với cạnh huyền)
=> AM = 1/2 . BC = 1/2. 5 = 2,5 (cm)
Chu vi hình thoi AEBM:
2,5 . 4 =10 (cm)
e) Nếu AEBM là hình vuông
thì Â= Ê= góc B= góc M= 90 độ
=>AM vuông góc BC
=> AM vừa là đường trung tuyến vừa là đường cao tam giác ABC
=> Tam giác ABC vuông cân tại A
Vậy tam giác ABC vuông cân ở A thì AEBM là hình vuông
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107742
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68485
Đã trả lời bởi chuyên gia
68485 -
 Đã trả lời bởi chuyên gia
52942
Đã trả lời bởi chuyên gia
52942 -
 Đã trả lời bởi chuyên gia
47433
Đã trả lời bởi chuyên gia
47433 -
 Đã trả lời bởi chuyên gia
45529
Đã trả lời bởi chuyên gia
45529 -
 Đã trả lời bởi chuyên gia
45189
Đã trả lời bởi chuyên gia
45189 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38558
Đã trả lời bởi chuyên gia
38558 -
 Đã trả lời bởi chuyên gia
38279
Đã trả lời bởi chuyên gia
38279


