a) Chứng minh rằng tứ giác AMCN là hình bình hành.
b) Gọi E và F lần lượt là trung điểm của AN và CM. Chứng minh rằng tứ giác DEFC là hình thang cân.
c) Gọi O là tâm đối xứng của hình chữ nhật ABCD, I và K lần lượt là hình chiếu của B và A trên CM. Chứng minh OI = OK.
Quảng cáo
3 câu trả lời 175
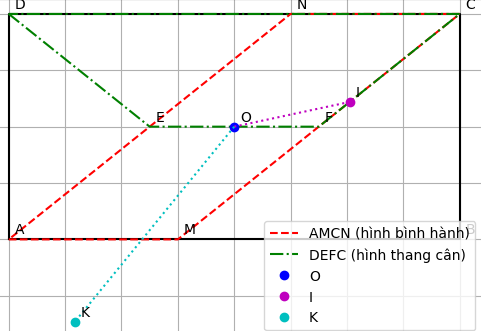
a) Chứng minh AMCN là hình bình hành
- Vì ABCD là hình chữ nhật nên: AB // CD, AD // BC
- Gọi AB = u, AD = v (vector). Khi đó:
M = A + λu, N = C + λu (λ = = )
- Tính các vector cạnh:
= M − A = λu, = N − C = λu
- Vì = → hai cạnh đối bằng nhau về phương và độ dài.
=> AMCN là hình bình hành.
b) Chứng minh DEFC là hình thang cân
- Gọi E, F là trung điểm của AN và CM: E = , F =
- Xét vector hai cạnh DE và CF:
= E − D = − D, 0 = F − C = − C = 2
- Sử dụng tính chất hình chữ nhật và AM = CN, ta thấy:
3
=> Tứ giác DEFC là hình thang cân.
c) Chứng minh OI = OK
- Tâm O của hình chữ nhật: O =4
- Hình chiếu của B và A lên CM: I = hình chiếu của B trên CM, K = hình chiếu của A trên CM
- Do O là tâm hình chữ nhật → O đối xứng qua CM → các hình chiếu của các đỉnh đối diện lên CM cách đều O
⇒ độ dài OI = OK
b) Để chứng minh DEFC là hình thang cân, ta cần chứng minh EF // DC và DE = FC, hoặc DE // FC và DE = FC.
c) Vì ABCD là hình chữ nhật nên tâm O là trung điểm của hai đường chéo AC và BD. Từ đó, ta có thể chứng minh O là trung điểm của IK, suy ra OI = OK.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107742
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68485
Đã trả lời bởi chuyên gia
68485 -
 Đã trả lời bởi chuyên gia
52942
Đã trả lời bởi chuyên gia
52942 -
 Đã trả lời bởi chuyên gia
47433
Đã trả lời bởi chuyên gia
47433 -
 Đã trả lời bởi chuyên gia
45529
Đã trả lời bởi chuyên gia
45529 -
 Đã trả lời bởi chuyên gia
45189
Đã trả lời bởi chuyên gia
45189 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38558
Đã trả lời bởi chuyên gia
38558 -
 Đã trả lời bởi chuyên gia
38279
Đã trả lời bởi chuyên gia
38279


