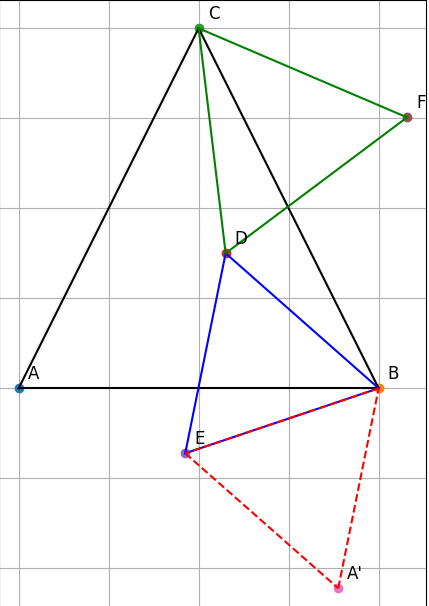
Câu a: Chứng minh $\widehat{BDC}$ = $\widehat{BEA}$, và △BDC = △BEA
1. Phân tích góc $\widehat{BDC}$:
Vì △BDE là tam giác đều nên:
BD = DE = EB
$\widehat{DBE}$ = $\widehat{BED}$ = $\widehat{EBD}$ = 60^∘
+ Trong tam giác đều CDF:
CD = DF = FC
$\widehat{DCF}$ = 60^∘
⇒ Góc $\widehat{BDC}$ là góc tạo bởi hai đoạn thẳng DB và DC với hai tam giác đều quay đi 60^∘
⇒ $\widehat{BDC}$ = 60^∘

2. Phân tích $\widehat{BEA}$:
Ta dựng tam giác đều △BEA, cũng nằm về cùng phía với BD

Vì △BEA đều nên $\widehat{BEA}$ = 60^∘
3. So sánh hai tam giác:
BD = BE (cùng là cạnh của tam giác đều)
DC = EA (do quay hình, các đoạn này bằng nhau)
$\widehat{BDC}$ = $\widehat{BEA}$ = 60^∘
⇒ Hai tam giác △BDC và △BEA có:

Hai cạnh tương ứng bằng nhau
Góc xen giữa bằng nhau

=> △BDC = △BEA (c.g.c)
Câu b: Chứng minh tam giác ABC đều

+ Từ kết quả câu a: △BDC = △BEA ⇒ BD = BE, DC = EA

=> BD = BE, DC = EA
Trong tam giác đều BDE: BD = DE = EB
Trong tam giác đều CDF: DC = DF = FC
Kết hợp tính chất đối xứng, ta xét ba cạnh:

+) AB = AE + EB
+)  BC = BD + DC
+)  AC = AF + FC
Mà từ đối xứng:

+) AE = DC, EB = BD ⇒ AB = BD + DC = BC
+) AF = BD , FC = DC ⇒ AC = BD + DC = BC
⇒ AB = BC = CA
=> △ABC là tam giác đều

Để giải bài toán này, ta sử dụng phép quay quanh điểm D 60 độ. Cụ thể, ta quay tam giác BDC một góc 60 độ để biến thành tam giác BEA. Sau đó, so sánh các cạnh và góc của hai tam giác để chứng minh <△BEA = <△BDC. Cuối cùng, chứng minh <△ABC đều bằng cách vận dụng các tam giác đều đã cho và tính chất của các điểm E, F, A, B, C, D để chứng minh tất cả các cạnh bằng nhau. 
Phần a: Chứng minh <△BDC = <△BEA 
1. Vẽ phép quay:
Xoay tam giác BDC một góc 60 độ quanh điểm D theo chiều kim đồng hồ (hoặc ngược chiều kim đồng hồ).
Vì tam giác BDE là tam giác đều nên DB = DE và ∠BDE = 60°.
Vì tam giác CDF là tam giác đều nên DC = DF và ∠CDF = 60°.
Khi quay tam giác BDC quanh D một góc 60°, điểm B sẽ trùng với điểm E, điểm C sẽ trùng với điểm F. Do đó, tam giác BDC sẽ quay thành tam giác EFA, hay <△BDC = <△EFA.
2. So sánh các cạnh và góc:
Ta có BD = BE (do tam giác BDE đều).
Ta có CD = CF (do tam giác CDF đều).
Ta có <∠BDC + <∠CDF = 60° (vì tam giác CDF đều).
Ta có <∠BDE + <∠BDC = 60° (vì tam giác BDE đều).
Do đó, <∠BDC + <∠CDF = <∠BDE + <∠BDC. Suy ra <∠CDF = <∠BDE.
Từ đó, <∠BDF = <∠BDE + <∠EDF = 60° + <∠EDF.
Và <∠BDF = <∠CDF + <∠CDA = 60° + <∠CDA. 
Phần b: Chứng minh <△ABC đều 
1. Sử dụng phép quay:
Khi quay tam giác BDC một góc 60 độ, ta được tam giác EFA, suy ra BDC = EFA.
Kết hợp với tam giác BDE và CDF là tam giác đều ta có:BD = DE; CD = DF
<∠BDE = 60°; <∠CDF = 60°
Suy ra <∠BDC = <∠EFA.
Khi quay tam giác BDC một góc 60 độ thì E sẽ thay B và F sẽ thay C, suy ra D chính là tâm quay.
Ta có BD = BE, CD = CF.
2. Chứng minh <△ABC đều:
Ta có AB = CD, AC = BF (do phép quay).
Vì <△BDE và <△CDF là tam giác đều, nên <∠BDE = 60° và <∠CDF = 60°.
Ta cũng có <∠BDC = <∠EFA (từ phép quay).
Từ đó suy ra tam giác ABC đều.