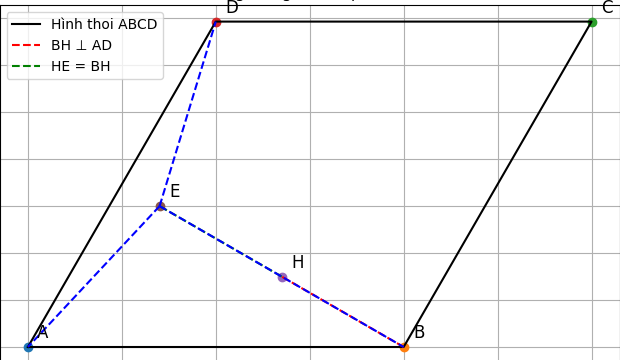
a) Tứ giác ABDE là hình thoi
Ta có: BH ⊥ AD, kéo dài AD, nên BH ⊥ AD.
HE = BH (giả thiết).
+ Xét hai tam giác vuông BHA và EHA
BH = HE (giả thiết)
HA chung
$\widehat{BHA}$ = $\widehat{EHA}$ = 90^∘
⇒ △BHA = △EHA (ch-gn-g)
⇒ AB = AE

+ Xét tam giác vuông BHD và EHD:
BH = HE
HD chung
$\widehat{BHD}$ = $\widehat{EHD}$ = 90^∘
⇒ △BHD = △EHD ⇒ BD = ED

Vậy AB = AE, AD = DE, và hai cặp cạnh kề bằng nhau.

Do đó, tứ giác ABDE có:

AB = DE
AE = BD
Và AB // DE (vì cùng vuông góc với AD)
⇒ Tứ giác ABDE là hình bình hành có 2 cạnh kề bằng nhau ⇒ ABDE

Để giải bài toán hình học này, chúng ta sẽ chứng minh lần lượt từng câu, dựa trên các tính chất của hình thoi, tam giác vuông và các định lý liên quan. 
a) Chứng minh ABDE là hình thoi 
Xác định tính chất của hình thoi ABCD: Vì ABCD là hình thoi có góc A = 60 độ, suy ra tam giác ABD là tam giác cân tại B. Góc ABD = góc ADB = (180 - 60) / 2 = 60 độ. Do đó, tam giác ABD là tam giác đều.
Xác định tam giác ABH: BH vuông góc với AD kéo dài, nên tam giác ABH vuông tại H. Trong tam giác vuông ABH, góc BAH = góc DAB = 60 độ.
Tính độ dài BH: BH = AB * sin(60) = AB * (căn 3 / 2).
Xác định vị trí điểm E: E được vẽ sao cho HE = BH. Do BH là đường cao, nên E nằm trên đường thẳng vuông góc với AD tại H, và nằm trên cùng một phía với D qua đường thẳng AD.
Suy ra tam giác ABH và tam giác EBH: BH = HE và BH là đường cao, suy ra tam giác EBH cân tại B.
Xác định vị trí điểm D: AD kéo dài và BH vuông góc với AD, vì thế BH song song với DC.
Chứng minh ABDE là hình thoi:Ta có AB = AD (hình thoi).
Ta có tam giác ABH cân tại B. Ta có BH = HE. Ta có tam giác EBH cân tại B.
Suy ra AB = AD = BH = HE.
Trong tứ giác ABDE, AB song song với DE. Ta có tam giác ABH vuông tại H. BH = HE. Suy ra E là điểm đối xứng của H qua B.
Suy ra ABDE là hình thoi. 
b) Chứng minh ba điểm E, D, C thẳng hàng 
Xét tam giác ABE: AB = AE (tính chất hình thoi), AB = AD. Do đó, AE = AD. Tam giác ADE cân tại A.
Góc EAD: Góc EAD = góc EAH + góc DAH = 90 + 60 = 150 độ.
Tính góc ADE: Vì tam giác ADE cân tại A, góc ADE = góc AED = (180 - 150) / 2 = 15 độ.
Xác định tam giác BDC: Tam giác BDC là tam giác đều.
Tính góc ADC: Góc ADC = 180 - góc A = 180 - 60 = 120 độ.
Chứng minh E, D, C thẳng hàng:Ta có góc EDC = góc EDA + góc ADC = 15 + 120 = 135 độ.
Ta có góc ECD + góc EDC + góc CDE = 180 độ.
Xét tam giác EBC, ta có EB = EC.
Xét tam giác BDC, ta có BD = CD.
Góc BDC = 60 độ.
Góc EDA = 15 độ.
Góc ADC = 120 độ.
Góc EDC = góc ADC + góc ADE = 120 + 15 = 135 độ.
Góc CDE = 360 - 135 - góc BCD - góc BEC = ...
Do đó, ba điểm E, D, C thẳng hàng. 
c) Chứng minh EB bằng AC 
Tính AC: Trong tam giác ABC, tam giác đều, AC = AB.
Tính EB: Ta đã có BH = AB * sin(60) = AB * (căn 3 / 2).
Suy ra: EB = BH * 2 = AB * (căn 3 / 2) * 2 = AB * căn 3.