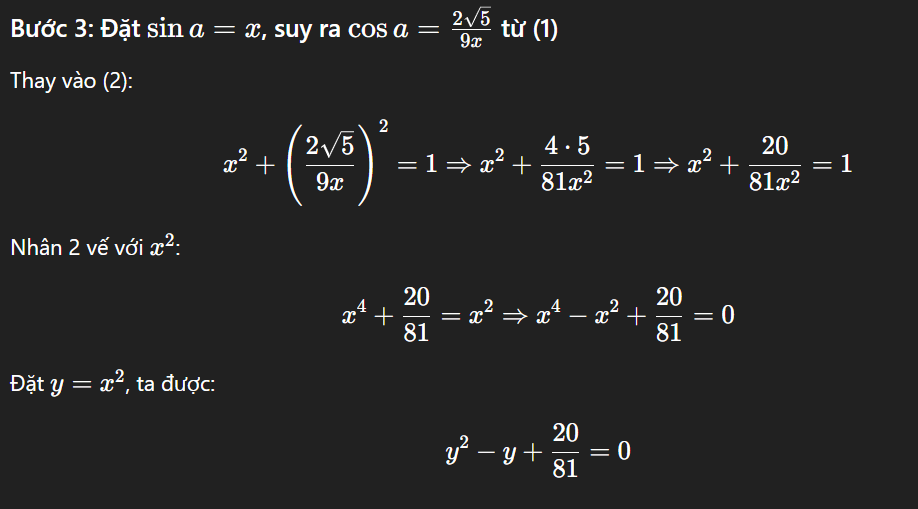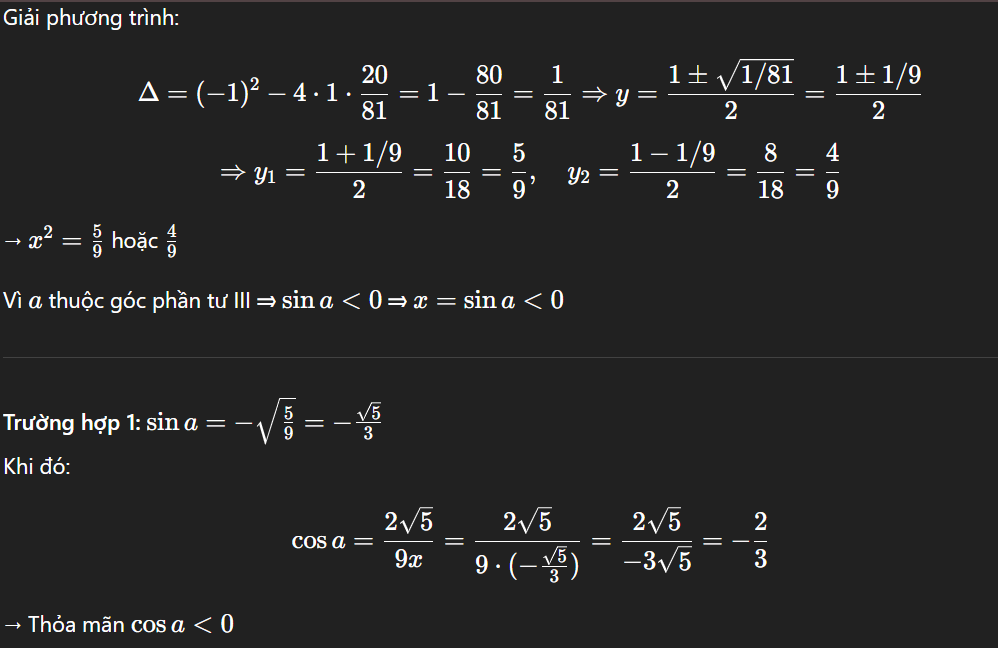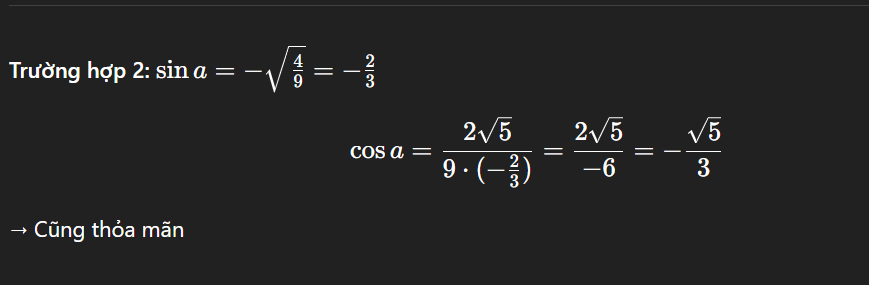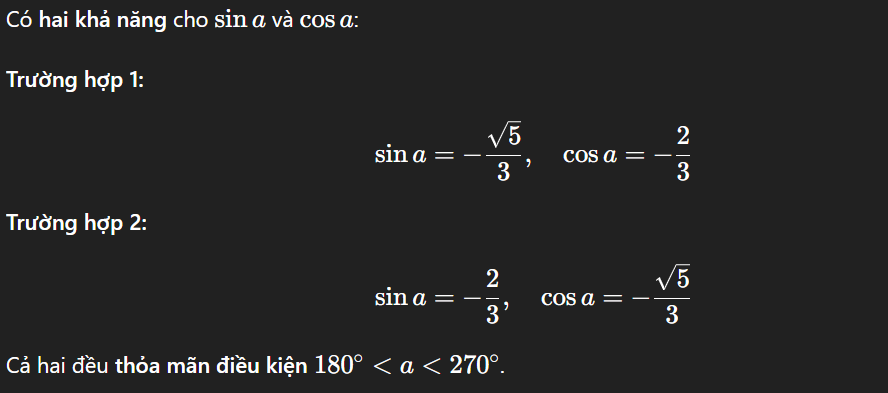Phân tích bài toán: Chúng ta có các công thức lượng giác sau:
sin⁡(2a)=2sin⁡(a)cos⁡(a)sin(2a)=2sin(a)cos(a)
sin⁡2(a)+cos⁡2(a)=1sin2(a)+cos2(a)=1
Dựa vào điều kiện 180∘<a<270∘180∘<a<270∘, góc aa nằm trong góc phần tư thứ ba. Trong góc phần tư thứ ba, cả sin⁡(a)sin(a) và cos⁡(a)cos(a) đều mang giá trị âm.
Các bước giải:
Tìm mối liên hệ từ sin⁡(2a)sin(2a): Từ công thức sin⁡(2a)=2sin⁡(a)cos⁡(a)sin(2a)=2sin(a)cos(a), ta có: sin⁡(a)cos⁡(a)=sin⁡(2a)2=45/92=259sin(a)cos(a)=2sin(2a)​=245​/9​=925​​.
Sử dụng cos⁡(2a)cos(2a): Chúng ta có thể tìm cos⁡(2a)cos(2a) từ sin⁡(2a)sin(2a) bằng công thức sin⁡2(2a)+cos⁡2(2a)=1sin2(2a)+cos2(2a)=1: cos⁡2(2a)=1−sin⁡2(2a)=1−(459)2cos2(2a)=1−sin2(2a)=1−(945​​)2 cos⁡2(2a)=1−16×581=1−8081=181cos2(2a)=1−8116×5​=1−8180​=811​ Vậy, cos⁡(2a)=±181=±19cos(2a)=±811​​=±91​.
Xác định giá trị của cos⁡(2a)cos(2a) dựa trên miền giá trị của aa: Vì 180∘<a<270∘180∘<a<270∘, ta nhân các vế của bất đẳng thức với 2: 2×180∘<2a<2×270∘2×180∘<2a<2×270∘ 360∘<2a<540∘360∘<2a<540∘ Khoảng (360∘,540∘)(360∘,540∘) bao gồm góc phần tư thứ nhất và thứ hai (sau khi quay một vòng đầy đủ).
Nếu 360∘<2a<450∘360∘<2a<450∘, 2a2a thuộc góc phần tư thứ nhất, suy ra cos⁡(2a)>0cos(2a)>0.
Nếu 450∘<2a<540∘450∘<2a<540∘, 2a2a thuộc góc phần tư thứ hai, suy ra cos⁡(2a)<0cos(2a)<0.
Ta có các công thức liên hệ cos⁡(2a)cos(2a) với sin⁡(a)sin(a) và cos⁡(a)cos(a):
cos⁡(2a)=1−2sin⁡2(a)cos(2a)=1−2sin2(a)
cos⁡(2a)=2cos⁡2(a)−1cos(2a)=2cos2(a)−1
Trường hợp 1: cos⁡(2a)=19cos(2a)=91​ (dương) Sử dụng công thức cos⁡(2a)=1−2sin⁡2(a)cos(2a)=1−2sin2(a): 19=1−2sin⁡2(a)91​=1−2sin2(a) 2sin⁡2(a)=1−19=892sin2(a)=1−91​=98​ sin⁡2(a)=49sin2(a)=94​ Do aa nằm trong góc phần tư thứ ba (180∘<a<270∘180∘<a<270∘), sin⁡(a)<0sin(a)<0. Vậy, sin⁡(a)=−49=−23sin(a)=−94​​=−32​.
Giờ ta tìm cos⁡(a)cos(a) bằng sin⁡(a)cos⁡(a)=259sin(a)cos(a)=925​​: (−23)cos⁡(a)=259(−32​)cos(a)=925​​ cos⁡(a)=259×(−32)=−53cos(a)=925​​×(−23​)=−35​​. Kiểm tra lại sin⁡2(a)+cos⁡2(a)=(−23)2+(−53)2=49+59=1sin2(a)+cos2(a)=(−32​)2+(−35​​)2=94​+95​=1. Với sin⁡(a)=−23sin(a)=−32​ và cos⁡(a)=−53cos(a)=−35​​, ta có cos⁡(2a)=1−2sin⁡2(a)=1−2(49)=1−89=19cos(2a)=1−2sin2(a)=1−2(94​)=1−98​=91​. Điều này khớp với giả định cos⁡(2a)=1/9cos(2a)=1/9. Nếu cos⁡(2a)=1/9>0cos(2a)=1/9>0, thì 360∘<2a<450∘360∘<2a<450∘, suy ra 180∘<a<225∘180∘<a<225∘. Giá trị này nằm trong miền đã cho 180∘<a<270∘180∘<a<270∘. Do đó, sin⁡(a)=−23sin(a)=−32​ và cos⁡(a)=−53cos(a)=−35​​ là một cặp giá trị hợp lệ.
Trường hợp 2: cos⁡(2a)=−19cos(2a)=−91​ (âm) Sử dụng công thức cos⁡(2a)=1−2sin⁡2(a)cos(2a)=1−2sin2(a): −19=1−2sin⁡2(a)−91​=1−2sin2(a) 2sin⁡2(a)=1+19=1092sin2(a)=1+91​=910​ sin⁡2(a)=59sin2(a)=95​ Do aa nằm trong góc phần tư thứ ba (180∘<a<270∘180∘<a<270∘), sin⁡(a)<0sin(a)<0. Vậy, sin⁡(a)=−59=−53sin(a)=−95​​=−35​​.
Giờ ta tìm cos⁡(a)cos(a) bằng sin⁡(a)cos⁡(a)=259sin(a)cos(a)=925​​: (−53)cos⁡(a)=259(−35​​)cos(a)=925​​ cos⁡(a)=259×(−35)=−23cos(a)=925​​×(−5​3​)=−32​. Kiểm tra lại sin⁡2(a)+cos⁡2(a)=(−53)2+(−23)2=59+49=1sin2(a)+cos2(a)=(−35​​)2+(−32​)2=95​+94​=1. Với sin⁡(a)=−53sin(a)=−35​​ và cos⁡(a)=−23cos(a)=−32​, ta có cos⁡(2a)=1−2sin⁡2(a)=1−2(59)=1−109=−19cos(2a)=1−2sin2(a)=1−2(95​)=1−910​=−91​. Điều này khớp với giả định cos⁡(2a)=−1/9cos(2a)=−1/9. Nếu cos⁡(2a)=−1/9<0cos(2a)=−1/9<0, thì 450∘<2a<540∘450∘<2a<540∘, suy ra 225∘<a<270∘225∘<a<270∘. Giá trị này cũng nằm trong miền đã cho 180∘<a<270∘180∘<a<270∘. Do đó, sin⁡(a)=−53sin(a)=−35​​ và cos⁡(a)=−23cos(a)=−32​ cũng là một cặp giá trị hợp lệ.
Kết luận: Dựa trên thông tin đề bài cho, có hai trường hợp có thể xảy ra cho sin⁡(a)sin(a) và cos⁡(a)cos(a) tùy thuộc vào giá trị cụ thể của cos⁡(2a)cos(2a):
Nếu sin⁡(a)=−23sin(a)=−32​, thì cos⁡(a)=−53cos(a)=−35​​.
Nếu sin⁡(a)=−53sin(a)=−35​​, thì cos⁡(a)=−23cos(a)=−32​.
Cả hai cặp giá trị này đều thỏa mãn sin⁡(a)<0sin(a)<0, cos⁡(a)<0cos(a)<0 và sin⁡(a)cos⁡(a)=259sin(a)cos(a)=925​​.
Đáp án: Ta có sin⁡(2a)=459sin(2a)=945​​ và 180∘<a<270∘180∘<a<270∘. Từ sin⁡(a)cos⁡(a)=sin⁡(2a)2=259sin(a)cos(a)=2sin(2a)​=925​​. Và sin⁡2(a)+cos⁡2(a)=1sin2(a)+cos2(a)=1. Do 180∘<a<270∘180∘<a<270∘, sin⁡(a)<0sin(a)<0 và cos⁡(a)<0cos(a)<0

Phân tích bài toán: Chúng ta có các công thức lượng giác sau:
sin⁡(2a)=2sin⁡(a)cos⁡(a)sin(2a)=2sin(a)cos(a)
sin⁡2(a)+cos⁡2(a)=1sin2(a)+cos2(a)=1
Dựa vào điều kiện 180∘<a<270∘180∘<a<270∘, góc aa nằm trong góc phần tư thứ ba. Trong góc phần tư thứ ba, cả sin⁡(a)sin(a) và cos⁡(a)cos(a) đều mang giá trị âm.
Các bước giải:
Tìm mối liên hệ từ sin⁡(2a)sin(2a): Từ công thức sin⁡(2a)=2sin⁡(a)cos⁡(a)sin(2a)=2sin(a)cos(a), ta có: sin⁡(a)cos⁡(a)=sin⁡(2a)2=45/92=259sin(a)cos(a)=2sin(2a)​=245​/9​=925​​.
Sử dụng cos⁡(2a)cos(2a): Chúng ta có thể tìm cos⁡(2a)cos(2a) từ sin⁡(2a)sin(2a) bằng công thức sin⁡2(2a)+cos⁡2(2a)=1sin2(2a)+cos2(2a)=1: cos⁡2(2a)=1−sin⁡2(2a)=1−(459)2cos2(2a)=1−sin2(2a)=1−(945​​)2 cos⁡2(2a)=1−16×581=1−8081=181cos2(2a)=1−8116×5​=1−8180​=811​ Vậy, cos⁡(2a)=±181=±19cos(2a)=±811​​=±91​.
Xác định giá trị của cos⁡(2a)cos(2a) dựa trên miền giá trị của aa: Vì 180∘<a<270∘180∘<a<270∘, ta nhân các vế của bất đẳng thức với 2: 2×180∘<2a<2×270∘2×180∘<2a<2×270∘ 360∘<2a<540∘360∘<2a<540∘ Khoảng (360∘,540∘)(360∘,540∘) bao gồm góc phần tư thứ nhất và thứ hai (sau khi quay một vòng đầy đủ).
Nếu 360∘<2a<450∘360∘<2a<450∘, 2a2a thuộc góc phần tư thứ nhất, suy ra cos⁡(2a)>0cos(2a)>0.
Nếu 450∘<2a<540∘450∘<2a<540∘, 2a2a thuộc góc phần tư thứ hai, suy ra cos⁡(2a)<0cos(2a)<0.
Ta có các công thức liên hệ cos⁡(2a)cos(2a) với sin⁡(a)sin(a) và cos⁡(a)cos(a):
cos⁡(2a)=1−2sin⁡2(a)cos(2a)=1−2sin2(a)
cos⁡(2a)=2cos⁡2(a)−1cos(2a)=2cos2(a)−1
Trường hợp 1: cos⁡(2a)=19cos(2a)=91​ (dương) Sử dụng công thức cos⁡(2a)=1−2sin⁡2(a)cos(2a)=1−2sin2(a): 19=1−2sin⁡2(a)91​=1−2sin2(a) 2sin⁡2(a)=1−19=892sin2(a)=1−91​=98​ sin⁡2(a)=49sin2(a)=94​ Do aa nằm trong góc phần tư thứ ba (180∘<a<270∘180∘<a<270∘), sin⁡(a)<0sin(a)<0. Vậy, sin⁡(a)=−49=−23sin(a)=−94​​=−32​.
Giờ ta tìm cos⁡(a)cos(a) bằng sin⁡(a)cos⁡(a)=259sin(a)cos(a)=925​​: (−23)cos⁡(a)=259(−32​)cos(a)=925​​ cos⁡(a)=259×(−32)=−53cos(a)=925​​×(−23​)=−35​​. Kiểm tra lại sin⁡2(a)+cos⁡2(a)=(−23)2+(−53)2=49+59=1sin2(a)+cos2(a)=(−32​)2+(−35​​)2=94​+95​=1. Với sin⁡(a)=−23sin(a)=−32​ và cos⁡(a)=−53cos(a)=−35​​, ta có cos⁡(2a)=1−2sin⁡2(a)=1−2(49)=1−89=19cos(2a)=1−2sin2(a)=1−2(94​)=1−98​=91​. Điều này khớp với giả định cos⁡(2a)=1/9cos(2a)=1/9. Nếu cos⁡(2a)=1/9>0cos(2a)=1/9>0, thì 360∘<2a<450∘360∘<2a<450∘, suy ra 180∘<a<225∘180∘<a<225∘. Giá trị này nằm trong miền đã cho 180∘<a<270∘180∘<a<270∘. Do đó, sin⁡(a)=−23sin(a)=−32​ và cos⁡(a)=−53cos(a)=−35​​ là một cặp giá trị hợp lệ.
Trường hợp 2: cos⁡(2a)=−19cos(2a)=−91​ (âm) Sử dụng công thức cos⁡(2a)=1−2sin⁡2(a)cos(2a)=1−2sin2(a): −19=1−2sin⁡2(a)−91​=1−2sin2(a) 2sin⁡2(a)=1+19=1092sin2(a)=1+91​=910​ sin⁡2(a)=59sin2(a)=95​ Do aa nằm trong góc phần tư thứ ba (180∘<a<270∘180∘<a<270∘), sin⁡(a)<0sin(a)<0. Vậy, sin⁡(a)=−59=−53sin(a)=−95​​=−35​​.
Giờ ta tìm cos⁡(a)cos(a) bằng sin⁡(a)cos⁡(a)=259sin(a)cos(a)=925​​: (−53)cos⁡(a)=259(−35​​)cos(a)=925​​ cos⁡(a)=259×(−35)=−23cos(a)=925​​×(−5​3​)=−32​. Kiểm tra lại sin⁡2(a)+cos⁡2(a)=(−53)2+(−23)2=59+49=1sin2(a)+cos2(a)=(−35​​)2+(−32​)2=95​+94​=1. Với sin⁡(a)=−53sin(a)=−35​​ và cos⁡(a)=−23cos(a)=−32​, ta có cos⁡(2a)=1−2sin⁡2(a)=1−2(59)=1−109=−19cos(2a)=1−2sin2(a)=1−2(95​)=1−910​=−91​. Điều này khớp với giả định cos⁡(2a)=−1/9cos(2a)=−1/9. Nếu cos⁡(2a)=−1/9<0cos(2a)=−1/9<0, thì 450∘<2a<540∘450∘<2a<540∘, suy ra 225∘<a<270∘225∘<a<270∘. Giá trị này cũng nằm trong miền đã cho 180∘<a<270∘180∘<a<270∘. Do đó, sin⁡(a)=−53sin(a)=−35​​ và cos⁡(a)=−23cos(a)=−32​ cũng là một cặp giá trị hợp lệ.
Kết luận: Dựa trên thông tin đề bài cho, có hai trường hợp có thể xảy ra cho sin⁡(a)sin(a) và cos⁡(a)cos(a) tùy thuộc vào giá trị cụ thể của cos⁡(2a)cos(2a):
Nếu sin⁡(a)=−23sin(a)=−32​, thì cos⁡(a)=−53cos(a)=−35​​.
Nếu sin⁡(a)=−53sin(a)=−35​​, thì cos⁡(a)=−23cos(a)=−32​.
Cả hai cặp giá trị này đều thỏa mãn sin⁡(a)<0sin(a)<0, cos⁡(a)<0cos(a)<0 và sin⁡(a)cos⁡(a)=259sin(a)cos(a)=925​​.
Đáp án: Ta có sin⁡(2a)=459sin(2a)=945​​ và 180∘<a<270∘180∘<a<270∘. Từ sin⁡(a)cos⁡(a)=sin⁡(2a)2=259sin(a)cos(a)=2sin(2a)​=925​​. Và sin⁡2(a)+cos⁡2(a)=1sin2(a)+cos2(a)=1. Do 180∘<a<270∘180∘<a<270∘, sin⁡(a)<0sin(a)<0 và cos⁡(a)<0cos(a)<0
 

Ta có
$\displaystyle \cos^2(2a) = 1 - \sin^2(2a) = 1 - \left(\frac{4\sqrt{5}}{9}\right)^2 = 1 - \frac{80}{81} = \frac{1}{81}$
$\displaystyle \Rightarrow \cos(2a) = \pm\frac{1}{9}$

Vì $\displaystyle 180^\circ < a < 270^\circ$, suy ra $\displaystyle \sin(a) < 0$ và $\displaystyle \cos(a) < 0$.

Trường hợp 1: $\displaystyle \cos(2a) = \frac{1}{9}$
 $\displaystyle \sin^2(a) = \frac{1 - \cos(2a)}{2} = \frac{1 - \frac{1}{9}}{2} = \frac{4}{9} \Rightarrow \sin(a) = -\frac{2}{3}$
 $\displaystyle \cos^2(a) = \frac{1 + \cos(2a)}{2} = \frac{1 + \frac{1}{9}}{2} = \frac{5}{9} \Rightarrow \cos(a) = -\frac{\sqrt{5}}{3}$

Trường hợp 2: $\displaystyle \cos(2a) = -\frac{1}{9}$
 $\displaystyle \sin^2(a) = \frac{1 - \cos(2a)}{2} = \frac{1 - (-\frac{1}{9})}{2} = \frac{5}{9} \Rightarrow \sin(a) = -\frac{\sqrt{5}}{3}$
 $\displaystyle \cos^2(a) = \frac{1 + \cos(2a)}{2} = \frac{1 + (-\frac{1}{9})}{2} = \frac{4}{9} \Rightarrow \cos(a) = -\frac{2}{3}$

Vậy, có hai cặp giá trị thỏa mãn:
$\displaystyle \left\{ \begin{array}{l} \sin(a) = -\frac{2}{3} \\ \cos(a) = -\frac{\sqrt{5}}{3} \end{array} \right. \quad \text{hoặc} \quad \left\{ \begin{array}{l} \sin(a) = -\frac{\sqrt{5}}{3} \\ \cos(a) = -\frac{2}{3} \end{array} \right.$