Bài 3: Cho tứ giác ABCD biết: góc A : góc B : góc C : góc D = 1 : 2 : 3 : 4.a) T

· 08:45 17/08/2025

Bài 3: Cho tứ giác ABCD biết: góc A : góc B : góc C : góc D = 1 : 2 : 3 : 4.
a) Tính các góc của tứ giác.
b) Chứng minh tứ giác ABCD là hình thang, AD song song BC.
c) Tính các góc của tam giác EDC (E là giao điểm của AC và BD).
Help em với ạ

Trả Lời (+5 điểm)

Hỏi chi tiết

Quảng cáo

2 câu trả lời 256

Gia Hân

3 tháng trước

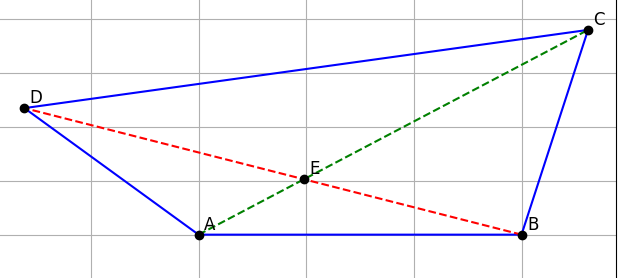
Hỏi đáp VietJack

a) Tính các góc của tứ giác
Trong tứ giác, tổng 4 góc luôn bằng:

$\hat{A}$ + $\hat{B}$ + $\hat{C}$ + $\hat{D}$ = 360^∘

Đặt: $\hat{A}$ = x ⇒ $\hat{B}$ = 2x, $\hat{C}$ = 3x, $\hat{D}$ = 4x

Ta có: x + 2x + 3x + 4x = 10x = 360^∘⇒ x = 36^∘

=> $\hat{A}$ = 36^∘, $\hat{B}$ = 72^∘ , $\hat{C}$ = 108^∘, $\hat{D}$ = 144^∘
b) Chứng minh ABCD là hình thang (AD // BC)

Xét: $\hat{A}$ + $\hat{D}$ = 36^∘+ 144^∘= 180^∘=> AD // BC

=> ABCD là hình thang (tứ giác có hai góc kề một cặp cạnh đối bằng nhau (tổng bằng 180°) thì hai cạnh đó song song)

c) Tính các góc của tam giác EDC, biết E là giao điểm của AC và BD
Gọi: $\hat{C}$ = 108^∘
E là giao điểm hai đường chéo AC và BD
Giả sử vẽ hình ABCD sao cho các đỉnh lần lượt theo chiều kim đồng hồ, bạn sẽ thấy tam giác EDC có 3 đỉnh là: E, D, và C.

Trong tam giác, tổng 3 góc luôn bằng: $\hat{B}$ 5 + $\hat{B}$ 6 + $\hat{B}$ 7 = 180^∘

Biết rằng góc $\hat{C}$ = $\hat{B}$ 6 + $\hat{B}$ 5 = 108^∘
Góc $\hat{D}$ = $\hat{B}$ 5 + $\hat{B}$ 7 = 144^∘

Giải hệ:

$\hat{B}$ 6 + $\hat{B}$ 5 = 108^∘(1)
$\hat{B}$ 7 + $\hat{B}$ 5 = 144^∘ (2)
$\hat{B}$ 6 + $\hat{B}$ 7 + $\hat{B}$ 5 = 180^∘ (3)
Trừ (1) và (2):
Từ (1): $\hat{B}$ 6 = 108^∘− $\hat{B}$ 5
Từ (2): $\hat{B}$ 7 = 144^∘− $\hat{B}$ 5

Thay vào (3):

(108^∘− $\hat{B}$ 5) + (144^∘− $\hat{B}$ 5) + $\hat{B}$ 5 = 180^∘

⇒ 252^∘− $\hat{B}$ 5 = 180^∘

⇒ $\hat{B}$ 5 = 72^∘

=> $\hat{B}$ 6 = 108^∘− 72^∘= 36^∘
$\hat{B}$ 7 = 144^∘− 72^∘= 72^∘

...Xem thêm

0 bình luận

Đăng nhập để hỏi chi tiết

♉︎𓍢🎧ＡＮ_Ｍê_ＯＴＰ_Dương _Ｈùng ✧˚.🎀༘⋆✧

3 tháng trước

Bài 3: Cho tứ giác ABCD biết tỉ lệ các góc là A∶B∶C∶D=1∶2∶3∶4

a) Tính các góc của tứ giác.
Tổng các góc trong một tứ giác là 360∘
.
Đặt các góc là x,2x,3x,4x
.
Ta có phương trình: x+2x+3x+4x=360∘
10x=360∘⇒x=36∘
.
Vậy các góc của tứ giác là: A=1⋅36∘=36
𝐵=2⋅36∘=72∘
C=3⋅36∘=108∘
D=4⋅36∘=144∘

b) Chứng minh tứ giác ABCD là hình thang, AD song song BC.
Để chứng minh ABCD là hình thang với AD∥, ta cần chứng minh tổng hai góc kề một cạnh bên bằng 180∘
.
Xét tổng hai góc A
và B
: A+B=36∘+72∘=108∘≠180∘
.
Xét tổng hai góc C
và D
: C+D=108∘+144∘=252∘≠180∘
∘
.
Xét tổng hai góc A
và D
: A+D=36∘+144∘=180∘
. Vì tổng hai góc trong cùng phía A
và D
bằng 180∘
, suy ra AB∥DC
.
Vậy tứ giác ABCD là hình thang với đáy là AB
và DC
.
Lưu ý:
Đề bài yêu cầu chứng minh AD∥BC
, nhưng theo tính toán, ta có AB∥DC
. Có thể đề bài có sự nhầm lẫn hoặc yêu cầu chứng minh một điều không đúng. Nếu đề bài đúng là AD∥BC
𝐴+𝐵=180∘
hoặc C+D=180∘
.

c) Tính các góc của tam giác EDC (E là giao điểm của AC và BD).
Với AB∥DC
, ta có: ∠BAC=∠DCA
(hai góc so le trong)
∠ABD=∠BDC
(hai góc so le trong)
Trong △EDC
: ∠EDC=∠BD
∠ECD=∠DCA
Để tính các góc của △EDC
, ta cần biết thêm thông tin về vị trí các đường chéo hoặc các góc cụ thể hơn. Với thông tin hiện có ( AB∥DC
𝐴𝐵∥𝐷𝐶
), ta chỉ biết được mối quan hệ giữa các góc so le trong. Không thể xác định chính xác giá trị của ∠DEC
nếu không có thêm dữ kiện.

Kết luận:
Các góc của tứ giác ABCD đã được tính ở phần a.
Tứ giác ABCD là hình thang với AB∥DC
, không phải AD∥BC
như đề bài yêu cầu ở phần b.
Không đủ thông tin để tính các góc của △EDC
ở phần c chỉ với việc E
là giao điểm của ACc
và BD
và AB∥DC

...Xem thêm

3 bình luận