Quảng cáo
3 câu trả lời 242
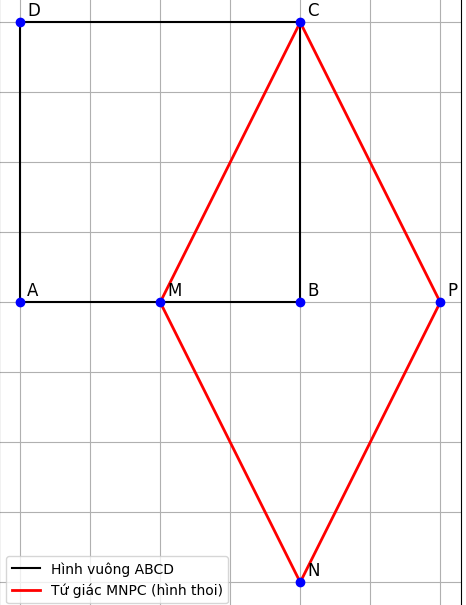
a) Chứng minh tứ giác MNPC là hình thoi
Vì M là trung điểm của AB nên: AM = MB
Lại có BP = BM (giả thiết)
⇒ Tam giác BMP cân tại B
⇒ MP = BM
Mà BM = AM ⇒ MP = AM
Lại có BC = BN (giả thiết)
⇒ Tam giác CBN cân tại B
⇒ CN = BC
Mà BC = AB = 2⋅AM ⇒ CN = 2AM
Vì MP = AM, nên: MP = AM = CN
Xét tứ giác MNPC, ta có:
MP = CN (vì đã chứng minh)
MN và PC đối xứng nhau qua đường chéo → bằng nhau
Tứ giác MNPC có bốn cạnh bằng nhau.
=> Tứ giác MNPC là hình thoi.
a)
Vì : M là trung điểm AB
Nên : BM=AM
P nằm trên tia MB và BM=BP nên ΔMBP cân tại B
Mà: MB=BP nên MP là đường trung tuyến ứng với cạnh đáy MB nên MP=MB
Tương tự ΔBCN có BN=BC nên tam giác BCN cân tại B
Do đó NC=NB
Vì MB=BP và BC=BN nên ta có MP=NC
Xét tứ giác MNPC có
MP=NC (chứng minh trên)
MP //NC vì cùng vuông góc với đường chéo BD của hình vuông
Tương tự ta c/m MN=PC và MN song song PC
Vậy MNPC là hình thoi
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
107278
-
Hỏi từ APP VIETJACK67830
-
44998
-
38171


