Cho góc xOy trên tia Ox lấy điểm A sao cho OA = 4 cm trên tia đối của tia Ox lấy điẻm B sao cho OB = 2cm đường trung trực của AB cắt AB tại H, M là 1 điểm trên đường trung trực đó . Các tia MB, AM lần lượt cắt Oy tại C và D, E là trung điểm của AC, F là trung điểm của BD .Chứng minh tam giác BOF, BAC , và AOE đồng dạng.
Quảng cáo
2 câu trả lời 184
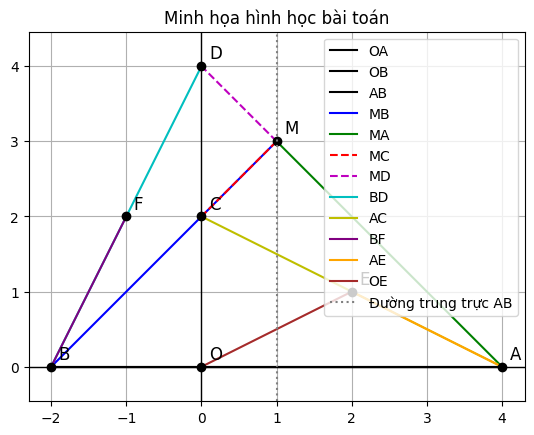
1. Chứng minh BOF ∼ BAC
Xét tam giác BAC và tam giác BOF.
Cùng có góc tại B chung.
Ta có E, F là trung điểm nên:
E trung điểm AC → AE = EC.
F trung điểm BD → BF = FD.
Đường trung trực của AB đi qua M nên M cách đều A và B.
Từ tính chất này, M là trung điểm trên đoạn thẳng song song tạo ra các tam giác có các cạnh tỉ lệ.
=> =
Góc B chung, tỉ số cạnh tương ứng bằng nhau, do đó: △BOF ∼ △BAC(góc - cạnh - góc)
2. Chứng minh △BAC ∼ △AOE
Xét tam giác BAC và tam giác AOE.
E là trung điểm của AC, O là gốc tọa độ.
AE là một đoạn thẳng nối trung điểm nên AE = EC.
Góc A chung ở hai tam giác.
Từ tính chất đường trung tuyến và tỉ số cạnh, ta có:
=
Do đó: △AOE ∼ △BAC(góc - cạnh - góc)
=> △BOF, △BAC, và △AOE đều đồng dạng với nhau theo tiêu chuẩn đồng dạng góc - cạnh - góc.
vẽ hình và c/m
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
107278
-
Hỏi từ APP VIETJACK67830
-
44998
-
38171


