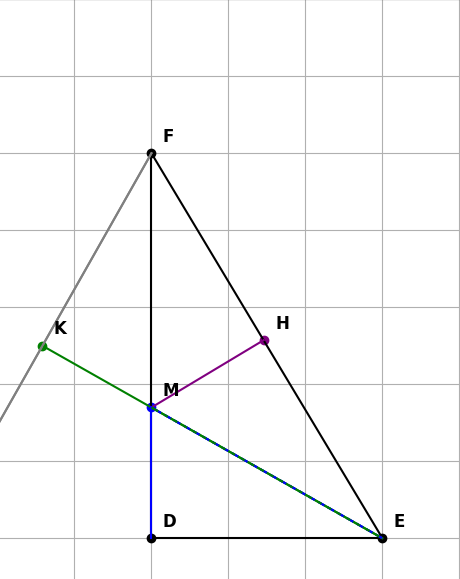
Cho A DEF vuông tai (DE <DF), kẻ tia phân giác của góc E cắt cạnh DF tạch, từ M kẻ NH vuông với EF lại H
a) chứng minh tam giácMHE=tam giácMDE ?
b) Chứng minh DM < MP ?
c) MH cắt tại DE tại A, EM cắt AF tại K Chứng minh EMvuông AF và tam giác AMF cân?
Quảng cáo
4 câu trả lời 196
= = 90∘(do cùng vuông góc với EF)
Chung cạnh ME
MH = MD do phân giác chia đoạn DF theo tỉ lệ
⇒ △MHE = △MDE (c.g.c)
Vì M nằm giữa D và F, và DF > DE (theo giả thiết)
Do phân giác nên M chia DF theo tỉ lệ < 1
⇒ DM < MF, mà MP là kéo dài từ M đến P (qua F) nên DM < MP
Khi đó:
Góc là nửa của góc (do EM là phân giác)
Góc vuông (do MH ⊥ EF và MH cắt DE tại A)
Tổng hai góc kề nhau:
+ = +
Mà là góc nhọn (< 90°) ⇒ < 45∘
= 90∘ ⇒ tổng hai góc là khoảng 135°, tức là tạo thành một hình gần vuông
=> EM ⊥ AF
+ Tứ giác AMHF có:
MH ⊥ EF (đã biết)
EM là phân giác
A nằm trên MH ⇒ có trục đối xứng qua MH
Do đó, hai đoạn AM và AF đối xứng qua đường thẳng MH
⇒ Tam giác AMF có hai cạnh bên bằng nhau: AM = AF
a) △MHE=△MDE
(cạnh huyền - góc nhọn).
b) DM<MP
.
c) (Không đủ thông tin để chứng minh EM⟂AF
và △AMF
cân).
a)
TG MHE= TG MDE(ch-cgn)
b)
Ta có 2 tam giác bằng nhau ở câu a
=>DM=HM(cạnh tương ứng)
Ta có MH vuông góc với EF
=> góc MHF =90 độ
Xét TG MHF có
góc MHF = 90 độ
=> TG MHF là TG vuông
=>MF>MH
mà MH=DM(CMT)
=>MF>MD
=>đpcm
câu c bạn viết lại đê bài rõ hơn cho mình nhé
*TG là Tam Giác nhé
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
107151
-
Hỏi từ APP VIETJACK67580
-
44957
-
38162


