trinhminhngoc2708@gmail.com
Hỏi từ APP VIETJACK
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC A (1;2;-1), B(2;-1;3), C (-2;3;3). Tìm tọa độ điểm D là chân đường phân giác trong góc A của tam giác.
Quảng cáo
3 câu trả lời 551
+ Độ dài các đoạn AB và AC
= B − A = (2 − 1, −1 − 2, 3 − ( −1)) = (1,−3,4)
=> =
= C − A = (−2 − 1, 3 − 2, 3 − (−1)) = (−3,1,4)
=> = = =
=> |AB| = |AC| = , tam giác này có hai cạnh bằng nhau
→ tam giác cân tại A
Điểm D nằm trên đoạn BC và chia đoạn BC theo tỉ số:
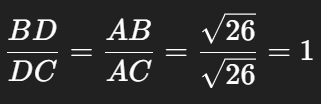
⇒ D là trung điểm của BC
Tọa độ trung điểm D của đoạn BC:
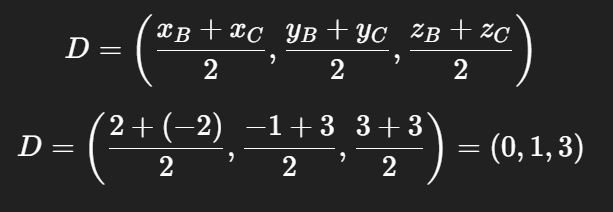
Vậy : D = (0, 1, 3)
4 tháng trước
Kết luận:
Tọa độ điểm D là chân đường phân giác trong góc A của tam giác là (0;1;3)
.
Tọa độ điểm D là chân đường phân giác trong góc A của tam giác là (0;1;3)
.
VEXITheEnlightener
· 4 tháng trước
:)? chỉ biết bám thôi à
♉︎𓍢🎧AN_Mê_OTP_Dương _Hùng ✧˚.🎀༘⋆✧
· 4 tháng trước
nói vậy là có ý gì
4 tháng trước
$\overrightarrow{AB} = (1; -3; 4) \Rightarrow AB = \sqrt{1^2 + (-3)^2 + 4^2} = \sqrt{26}$
$\overrightarrow{AC} = (-3; 1; 4) \Rightarrow AC = \sqrt{(-3)^2 + 1^2 + 4^2} = \sqrt{26}$
Ta có: $D$ là chân đường phân giác trong của $\widehat{A}$
$\Rightarrow \dfrac{BD}{CD} = \dfrac{AB}{AC} = \dfrac{\sqrt{26}}{\sqrt{26}} = 1$
$\Rightarrow BD = CD$
$\Rightarrow D$ là trung điểm $BC$
$\Rightarrow D\left(\dfrac{2 - 2}{2}; \dfrac{-1 + 3}{2}; \dfrac{3 + 3}{2}\right)$
$\Rightarrow D(0; 1; 3)$
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
Gửi báo cáo thành công!



