Quảng cáo
3 câu trả lời 212
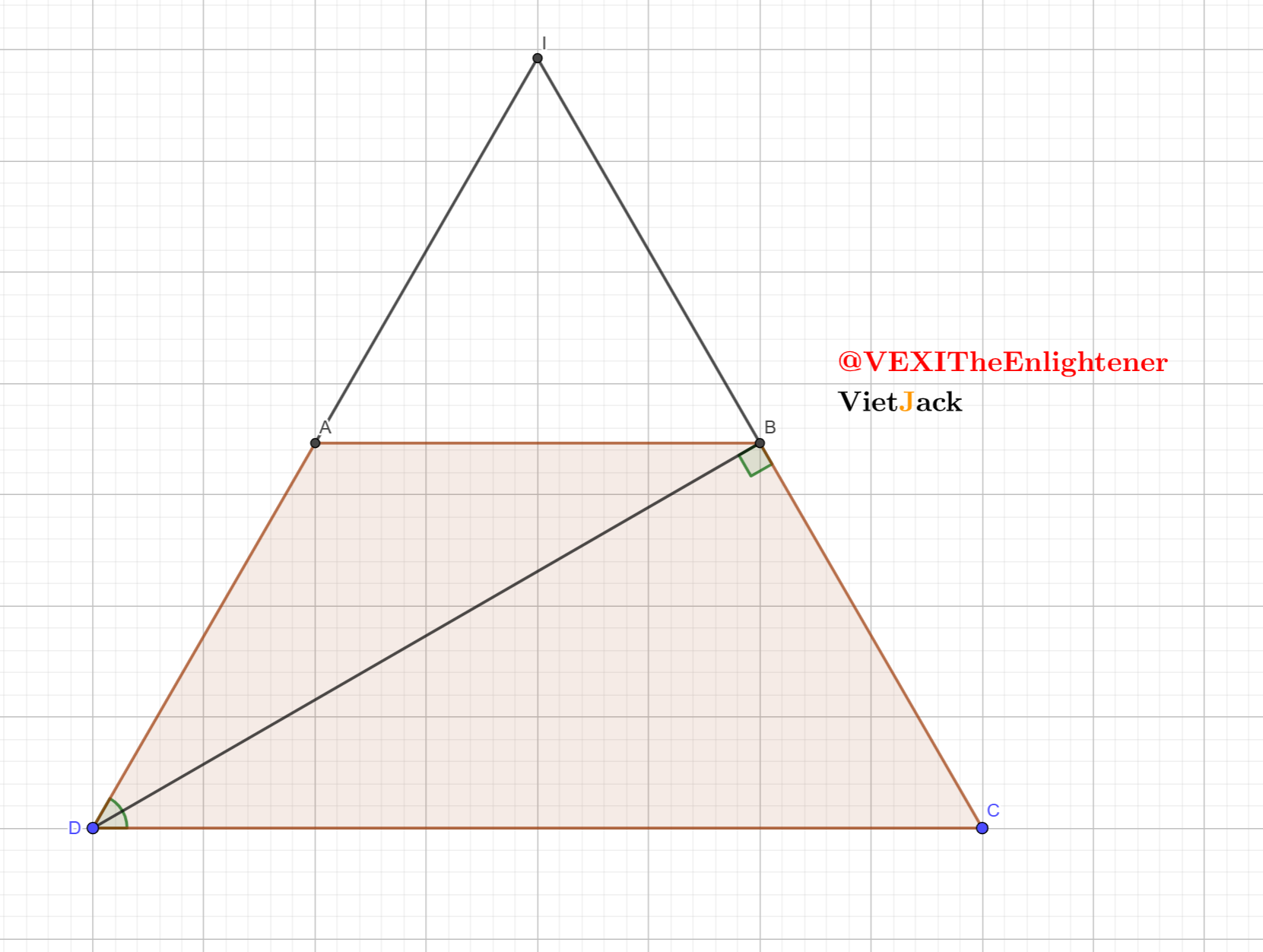
Ta có:
$\begin {cases} \widehat{ABD} = \widehat{BDC} (AB // CD) \\ \widehat{ADB} = \widehat{BDC} (BD\text{ là phân giác của }\widehat{ADC}) \end {cases}$
$\Rightarrow \widehat{ABD} = \widehat{ADB}$
$\Rightarrow \triangle ABD$ cân tại $A$
$\Rightarrow AD = AB = 4(cm)$
Mà $BC = AD (ABCD$ là hình thang cân$)$
$\Rightarrow BC = 4(cm)$
Ta có: $\triangle BCD$ vuông tại $B$
$\Rightarrow \widehat{BDC} + \widehat{BCD} = 90^\circ$
Mà $\widehat{BCD} = \widehat{ADC} (ABCD$ là hình thang cân$)$
$\phantom{Mà} \widehat{ADC} = 2\widehat{BDC} (BD$ là phân giác của $\widehat{ADC})$
$\Rightarrow \widehat{BDC} + 2\widehat{BDC} = 90^\circ$
$\Rightarrow \widehat{BDC} = 30^\circ$
$\Rightarrow \widehat{ADC} = \widehat{BCD} = 60^\circ$
Gọi $I$ là giao điểm của $AD$ và $BC$
$\Rightarrow \triangle ICD$ đều $(2$ góc kề một đáy bằng nhau và bằng $60^\circ)$
$\Rightarrow ID = IC = CD$
Ta có: $\triangle ICD$ đều
$\Rightarrow \triangle ICD$ cân tại $D$
Mà $BD$ là phân giác của $\widehat{IDC}(\text{gt})$
$\Rightarrow BD$ là đường trung tuyến của $\triangle ICD$
$\Rightarrow B$ là trung điểm của $IC$
$\Rightarrow IC = 2BC = 8(cm)$
$\Rightarrow CD = IC = 8(cm)$
$\Rightarrow$ Chu vi của $ABCD$ là $AB + BC + CD + AD = 4 + 4 + 8 + 4 = 20(cm)$
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
107151
-
Hỏi từ APP VIETJACK67580
-
44957
-
38162
-
돈이없다 💸😭
435 điểm
-
반짝이는 달 420 điểm
-
야연 ✨
400 điểm
-
보고 싶어요
385 điểm
-
jet jet #
345 điểm
-
౨ৎ𝘉ắ𝘱ت𝘭𝘶ộ𝘤تđê⋅˚₊‧ ଳ⋆.࿔*:･🌽
305 điểm
-
`d.`
285 điểm
-
Kiều Anh 170 điểm
-
Phát: ''đạp = niềm tin hả?''; t : ''🤫🧏''
135 điểm
-
`color{blue}text{이 글을 읽는 사람은 바보다.`베트남이 챔피언입니다.
105 điểm
-
Hung Hungdoan 100 điểm
-
baolam<3
70 điểm
-
Paris.khong.co.em...
70 điểm
-
Judy Hopps
60 điểm
Rút gọn
Bài viết mới nhất Lớp 8
-
3 năm trước8199
-
3 năm trước7715
-
3 năm trước6553
-
3 năm trước6447
-
3 năm trước6270
