Quảng cáo
3 câu trả lời 331
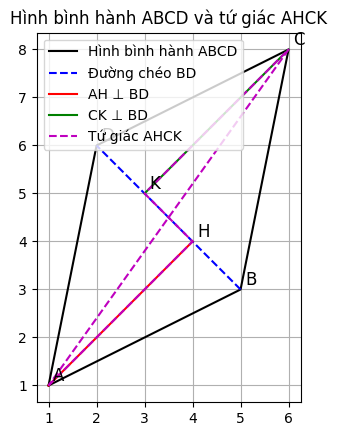
+ Xét 2 đoạn thẳng AH và CK:
AH ⊥ BD, CK ⊥ BD (1)
AH ⊥ BD, CK ⊥ BD (1)
⇒ AH // CK (cùng vuông góc với 1 đường thẳng).
+ Vì ABCD là hình bình hành
+ Vì ABCD là hình bình hành
⇒ AB // CD, và AB = CD.
Góc giữa AB với BD bằng góc giữa CD với BD
Góc giữa AB với BD bằng góc giữa CD với BD
⇒ Tam giác vuông ABH và CDK bằng nhau
⇒ AH = CK(2)
c. Từ (1) và (2): AH // CK và AH = CK
c. Từ (1) và (2): AH // CK và AH = CK
⇒ Hai cạnh đối song song và bằng nhau.
+ Tương tự, HC // AK và HC = AK
+ Tương tự, HC // AK và HC = AK
⇒ AHCK là hình bình hành.
4 tháng trước
Vì AH // CK và AH = CK, nên tứ giác AHCK là hình bình hành.
Vậy, tứ giác AHCK là hình bình hành.
Vậy, tứ giác AHCK là hình bình hành.
VEXITheEnlightener
· 4 tháng trước
chứng minh??
4 tháng trước
Vì AH // CK và AH = CK, nên tứ giác AHCK là hình bình hành.
Vậy, tứ giác AHCK là hình bình hành.
Vậy, tứ giác AHCK là hình bình hành.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
107278
-
Hỏi từ APP VIETJACK67830
-
44998
-
38171
Gửi báo cáo thành công!


