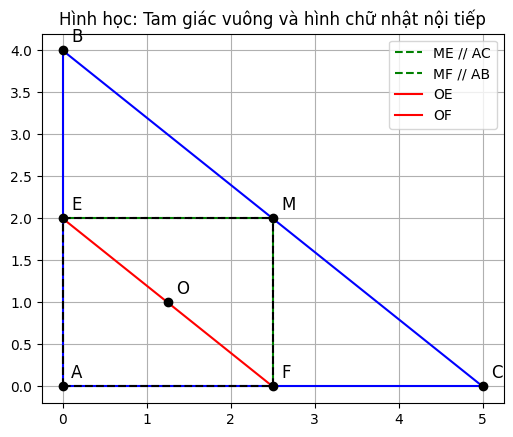
cho tam giác ABC vuông tại A, gọi M là trung điểm của BC .Tư M kẻ ME // AC (E thuộc AB ), MF // AB ( F thuộc AC) a, Chứng minh tứ giác BEFM là hình bình hành b, C/m tứ giác AEMF là hình chữ nhật c, Gọi O là trung điểm của AM . chứng minh OE = OF
Quảng cáo
3 câu trả lời 1485
Tam giác ABC vuông tại A => = 90∘.
Do MF // AB, ME // AC, nên MF ⊥ ME.
=> Các cạnh kề của tứ giác AEMF vuông góc nhau.
=> Tứ giác AEMF là hình bình hành có một góc vuông.
=> AEMF là hình chữ nhật (vì là hình bình hành có một góc vuông).
c) Chứng minh OE = OF
Xét hai tam giác △OME và △OMF:
OM chung
ME = MF (vì hình chữ nhật AEMFAEMFAEMF có hai cạnh đối bằng nhau)
= = 90∘(vì góc tại M của hình chữ nhật là vuông)
⇒ Hai tam giác △OME và △OMF bằng nhau theo trường hợp cạnh – góc vuông – cạnh (c.g.c).
⇒ OE = OF (hai cạnh tương ứng).
Vậy: OE=OF (đpcm)
Đề bài cho tam giác ABC vuông tại A, M là trung điểm của BC. Từ M kẻ ME // AC (E thuộc AB), MF // AB (F thuộc AC).
a, Chứng minh tứ giác BEFM là hình bình hành
Để chứng minh BEFM là hình bình hành, ta cần chứng minh hai cặp cạnh đối song song hoặc bằng nhau.
Ta có:ME // AC (theo giả thiết) mà AC lại song song với AB (vì A là góc vuông). Tuy nhiên, ở đây ta cần ME // AB chứ không phải song song với AC. Hãy xem lại giả thiết: "ME // AC (E thuộc AB)". Điều này có nghĩa là đoạn ME song song với cạnh AC.
Do ME // AC và AC là một phần của đường thẳng AC, nên ME // AC.
Mà AB vuông góc với AC (vì tam giác ABC vuông tại A).
Vì ME // AC, mà AB vuông góc với AC, suy ra AB vuông góc với ME.
Cần xem lại giả thiết ME // AC (E thuộc AB). Điều này có nghĩa là ME song song với đường thẳng AC.
Ta có AB vuông góc với AC (do tam giác ABC vuông tại A).
Nếu ME // AC và AB vuông góc với AC, thì ME cũng vuông góc với AB. Điều này mâu thuẫn với việc E thuộc AB, trừ khi ME trùng với điểm A hoặc B.
Có lẽ đề bài muốn nói ME // AC và E thuộc AB. Vậy ME song song với AC.
MF // AB và F thuộc AC. Vậy MF song song với AB.
Xét tứ giác BEFM:
ME // AC (giả thiết). Vì F thuộc AC, nên ME // FC.
MF // AB (giả thiết). Vì E thuộc AB, nên MF // EB.
Vậy, tứ giác BEFM có các cặp cạnh đối song song (ME // FC và MF // EB).
Do đó, tứ giác BEFM là hình bình hành.
b, Chứng minh tứ giác AEMF là hình chữ nhật
Để chứng minh AEMF là hình chữ nhật, ta cần chứng minh nó là hình bình hành và có một góc vuông.
Ta đã chứng minh tứ giác BEFM là hình bình hành ở câu a.
Xét tứ giác AEMF:
ME // AC (giả thiết). Vì F thuộc AC, nên ME // AF.
MF // AB (giả thiết). Vì E thuộc AB, nên MF // AE.
Vậy, tứ giác AEMF có các cặp cạnh đối song song (ME // AF và MF // AE). Do đó, AEMF là hình bình hành.
Bây giờ ta cần chứng minh một góc vuông.
Ta có tam giác ABC vuông tại A, nên góc BAC = 90 độ.
Trong hình bình hành AEMF, góc AEM là góc EAB (do ME // AC và cắt AB) và góc AFM là góc FAE (do MF // AB và cắt AC).
Ta có:
ME // AC và E thuộc AB. EF là đường thẳng song song với AC cắt AB tại E.
MF // AB và F thuộc AC. ME là đường thẳng song song với AB cắt AC tại F.
Xem lại giả thiết và hình vẽ: ME // AC và E thuộc AB. MF // AB và F thuộc AC.
Vì ME // AC, mà AB vuông góc với AC (do tam giác ABC vuông tại A), suy ra ME vuông góc với AB. Do đó, góc AEM = 90 độ.
Vì MF // AB, mà AC vuông góc với AB (do tam giác ABC vuông tại A), suy ra MF vuông góc với AC. Do đó, góc AFM = 90 độ.
Hoặc đơn giản hơn: E nằm trên AB, F nằm trên AC. ME // AC và MF // AB.
Do E thuộc AB và MF // AB, MF vuông góc với AC (vì AC vuông góc với AB). Vậy góc AFM = 90 độ.
Do F thuộc AC và ME // AC, ME vuông góc với AB (vì AB vuông góc với AC). Vậy góc AEM = 90 độ.
Ta đã có AEMF là hình bình hành.
Trong hình bình hành AEMF, có góc FAE = góc BAC = 90 độ (vì E thuộc AB, F thuộc AC).
Một hình bình hành có một góc vuông là hình chữ nhật.
Do đó, tứ giác AEMF là hình chữ nhật.
c, Gọi O là trung điểm của AM. Chứng minh OE = OF
Để chứng minh OE = OF, ta có thể sử dụng tính chất của hình chữ nhật hoặc các tam giác bằng nhau.
Cách 1: Sử dụng tính chất đường chéo của hình chữ nhật
Ta đã chứng minh AEMF là hình chữ nhật ở câu b.
Trong hình chữ nhật AEMF, hai đường chéo là AM và EF.
Hai đường chéo của hình chữ nhật bằng nhau và cắt nhau tại trung điểm của mỗi đường.
O là trung điểm của AM (theo giả thiết).
Vì AEMF là hình chữ nhật, tâm đối xứng của nó là giao điểm hai đường chéo, tức là trung điểm của AM và EF.
Do O là trung điểm của AM, nên O cũng là trung điểm của EF.
Vì O là trung điểm của EF, nên OE = OF = EF/2.
Do đó, OE = OF.
Cách 2: Sử dụng tính chất trung điểm trong tam giác
Xét tam giác ABM:
Ta có E là trung điểm của AB (cần chứng minh).
Ta có M là trung điểm của BC. ME // AC. Vì AC // MF, ME // AC.
Trong tam giác ABC, M là trung điểm BC, ME // AC, E thuộc AB. Theo định lý đường trung bình, E là trung điểm của AB.
Trong tam giác ABC, M là trung điểm BC, MF // AB, F thuộc AC. Theo định lý đường trung bình, F là trung điểm của AC.
Vậy E là trung điểm AB, F là trung điểm AC.
Xét tam giác ABM: E là trung điểm của AB. O là trung điểm của AM.
Theo định lý đường trung bình trong tam giác ABM, đoạn thẳng OE nối trung điểm hai cạnh AB và AM sẽ song song với cạnh thứ ba (BM) và bằng một nửa cạnh đó: OE = 1/2 BM.
Xét tam giác ACM: F là trung điểm của AC. O là trung điểm của AM.
Theo định lý đường trung bình trong tam giác ACM, đoạn thẳng OF nối trung điểm hai cạnh AC và AM sẽ song song với cạnh thứ ba (CM) và bằng một nửa cạnh đó: OF = 1/2 CM.
Ta biết M là trung điểm của BC, nên BM = CM = 1/2 BC.
Từ OE = 1/2 BM và OF = 1/2 CM, ta có:
OE = 1/2 (1/2 BC) = 1/4 BC
OF = 1/2 (1/2 BC) = 1/4 BC
Do đó, OE = OF.
✅ Kết quả ngắn gọn:
a) Tứ giác BEFM\boxed{BEFM} là hình bình hành
b) Tứ giác AEMF\boxed{AEMF} là hình chữ nhật
c) OE=OF\boxed{OE = OF}
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107437
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68061
Đã trả lời bởi chuyên gia
68061 -
 Đã trả lời bởi chuyên gia
52846
Đã trả lời bởi chuyên gia
52846 -
 Đã trả lời bởi chuyên gia
47344
Đã trả lời bởi chuyên gia
47344 -
 Đã trả lời bởi chuyên gia
45400
Đã trả lời bởi chuyên gia
45400 -
 Đã trả lời bởi chuyên gia
45045
Đã trả lời bởi chuyên gia
45045 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38412
Đã trả lời bởi chuyên gia
38412 -
 Đã trả lời bởi chuyên gia
38191
Đã trả lời bởi chuyên gia
38191


