a) ΔBDE = ΔICD
b) BE ⊥ ID
Quảng cáo
3 câu trả lời 518
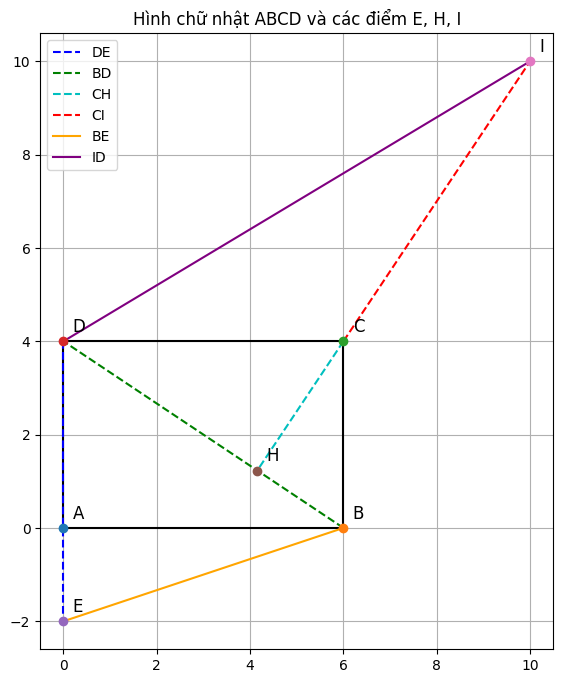
a, Chứng minh: ΔBDE = ΔICD
Xét hai tam giác △BDE và △ICD, ta có :
DE = DC (giả thiết)
BD = CI (giả thiết)
Góc giữa BD và DE bằng góc giữa DC và CI
Vì H là hình chiếu của C lên BD, CH⊥BD , nên góc giữa CH và BD là 90∘
Mà CI là đối của tia CH nên cũng tạo góc 90∘ với BD, nhưng ngược chiều.
→ =
✅ Do đó: △BDE = △ICD (c-g-c)
b, Chứng minh: BE ⊥ ID
Từ câu a, hai tam giác BDE và ICD bằng nhau, nên:
BE = ID (do là cạnh tương ứng)
Góc giữa BE và BD bằng góc giữa ID và CD
Mà BE nằm trên tam giác vuông BDE, ID nằm trong tam giác ICD đối xứng qua đường chéo
⇒ BE ⊥ ID (đpcm)
a) Để chứng minh △BDE=△ICD, ta thực hiện các bước sau:
Xét tứ giác DECI.
Chứng minh DE=CI và BD=IC.
Chứng minh ∠BDE=∠ICD=90∘+∠BDC.
Suy ra △BDE=△ICD (c.g.c).
b) Để chứng minh BE⊥ID, ta thực hiện các bước sau:
Từ △BDE=△ICD, suy ra ∠EBD=∠DIC.
Gọi K là giao điểm của BE và ID.
Xét △KBD và △HCD.
Ta có ∠HCD=∠CBD (cùng phụ với ∠BDC) và ∠DIC=∠CBD.
Do đó, ∠DIC=∠HCD.
Xét △KBC, ta có ∠BKC+∠KBC+∠BCK=180∘.
Ta có ∠KBC+∠BCK=∠CBD+∠HCD=90∘.
Suy ra ∠BKC=90∘.
Do đó, BE⊥ID.
Quảng cáo
Bạn hỏi - Chuyên gia trả lời
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
114078
-
Hỏi từ APP VIETJACK74946
-
Đã trả lời bởi chuyên gia
54732 -
48105
-
39905
-
uk
615 điểm
-
Nga Nguyễn Thanh 415 điểm
-
`color{lightpink}text{bbao}`
385 điểm
-
tóc vàng mắt xanh
315 điểm
-
meoz
295 điểm
-
ll950
220 điểm
-
`color{ pink}text{hoàng tử rau má}`
155 điểm
-
Min Ni
150 điểm
-
iu cô hằng xin cô 1 slot nx vs (22k điểm trc)
140 điểm
-
`color{ pink}text{ha my}`
140 điểm
-
anh zai nek
135 điểm
-
$\forall$$\textit{Đức!?}$$\mathbb{Z}$ 130 điểm
-
Bố chúng mày
120 điểm
-
$\color{#c799f2}{Cô Hằng VietJack}$
105 điểm
-
$\Huge\color{magenta}{PIPILABU}$
100 điểm
Rút gọn
Bài viết mới nhất Lớp 8
-
4 năm trước10792
-
4 năm trước10198
-
4 năm trước8867
-
4 năm trước9047
-
4 năm trước8606
