Bài 17. Cho hình thang ABCD (AB // CD, AD ≠ BC). Gọi E, F lần lượt là trung điểm của các đường chéo BD, AC và G là giao điểm của đường thẳng qua E vuông góc với AD và đường thẳng qua F vuông góc với BC.
Chứng minh rằng GD = GC.
Bài 18. Cho hình thang cân ABCD đáy nhỏ AB. Độ dài đường cao BH bằng độ dài đường trung bình của hình thang ABCD.
Chứng minh rằng BD vuông góc với AC
please,cần gấp ạ huhu
Quảng cáo
2 câu trả lời 209
Bài 1:
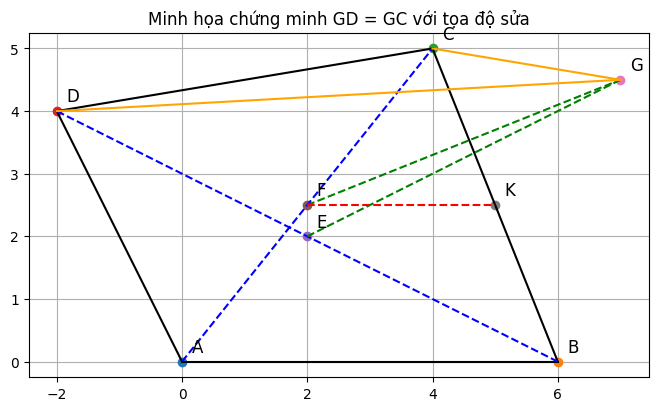
Gọi K trung điểm BC
=> KF//AD (trung bình của tg DAC)
=> EG vuông góc KF (vì EG vuông góc AD), tương tự EK//BC và FG vuông góc FE
=>G là trực tâm tam giác EFK
=> GK vuông góc EF
=> GK vuông góc DC vì FE//DC (nối trung điểm 2 dường chéo của hình thang thuộc đường trung bình hình thang)
=> GK trung trực DC
=> tg GDC cân tại G
=> GD = GC (đpcm)
=> KF//AD (trung bình của tg DAC)
=> EG vuông góc KF (vì EG vuông góc AD), tương tự EK//BC và FG vuông góc FE
=>G là trực tâm tam giác EFK
=> GK vuông góc EF
=> GK vuông góc DC vì FE//DC (nối trung điểm 2 dường chéo của hình thang thuộc đường trung bình hình thang)
=> GK trung trực DC
=> tg GDC cân tại G
=> GD = GC (đpcm)
Bài 2:
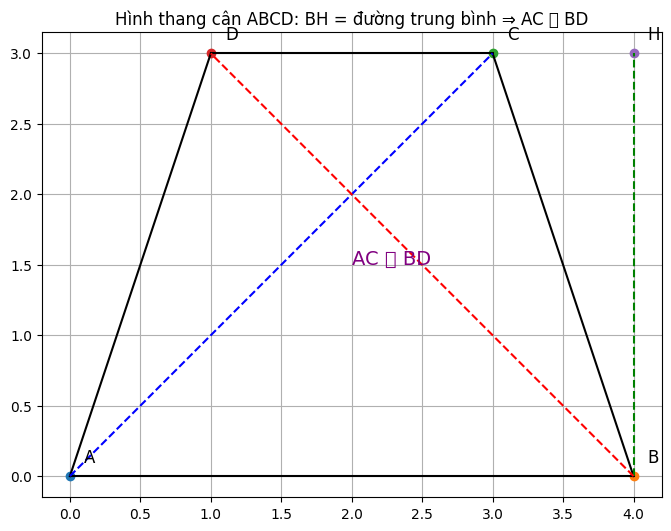
Đường trung bình MN = BH.
Từ BH và hình thang cân, tính được DH = (CD − AB) / 2.
Xét tam giác vuông BHD, tính được BD2 = BH2 + DH2.
Tương tự, tính được AC2.
Do AC = BD, nên tam giác tạo bởi giao điểm đường chéo và đáy là tam giác vuông cân.
Kết luận: AC ⊥ BD.
Từ BH và hình thang cân, tính được DH = (CD − AB) / 2.
Xét tam giác vuông BHD, tính được BD2 = BH2 + DH2.
Tương tự, tính được AC2.
Do AC = BD, nên tam giác tạo bởi giao điểm đường chéo và đáy là tam giác vuông cân.
Kết luận: AC ⊥ BD.
4 tháng trước
5. Kết nối các yếu tố và chứng minh:
Sử dụng các mối quan hệ về độ dài cạnh và đường cao để chứng minh rằng tam giác có cạnh là đường chéo và đường cao sẽ dẫn đến kết quả vuông góc.
Cụ thể, chứng minh rằng AC2+BD2=(AB+CD)2
hoặc một mối quan hệ tương tự để suy ra BD vuông góc với AC.
Sử dụng các mối quan hệ về độ dài cạnh và đường cao để chứng minh rằng tam giác có cạnh là đường chéo và đường cao sẽ dẫn đến kết quả vuông góc.
Cụ thể, chứng minh rằng AC2+BD2=(AB+CD)2
hoặc một mối quan hệ tương tự để suy ra BD vuông góc với AC.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
107278
-
Hỏi từ APP VIETJACK67830
-
44998
-
38171
Gửi báo cáo thành công!


