Cho hình thang ABCD (AB//CD) có AC = BD. Qua B kẻ đường thẳng song song với AC, cắt đường thẳng DC tại E. Chứng minh:
a, ΔBDE là tam giác cân.
b, ΔACD = ΔBDC.
c, Hình thang ABCD là hình thang cân.
Quảng cáo
3 câu trả lời 1166
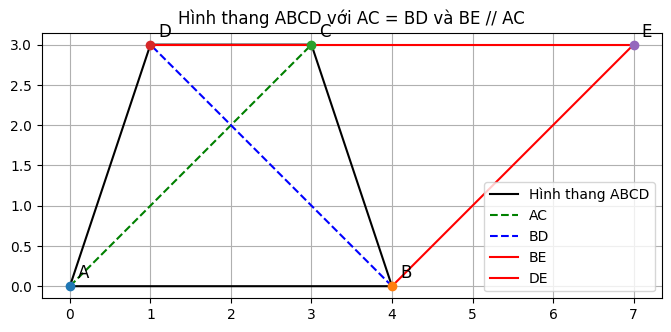
Tam giác △BDE có hai cạnh bằng nhau: BE = DE (do đối xứng theo song song)
→ △BDE cân tại E (đpcm)
DC chung
= (so le trong vì AB // CD)
→ tam giác ACD = tam giác BDC (c.g.c)
→ Hình thang ABCD có hai cạnh bên bằng nhau ⇒ ABCD là hình thang cân (đpcm)
Phân tích đề bài và Dựng hình
Cho hình thang ABCD với AB∥CD. Đường chéo AC=BD. Kẻ đường thẳng qua B song song với AC, cắt đường thẳng DC tại E.
a) Chứng minh: △BDE là tam giác cân.
Để chứng minh △BDE là tam giác cân, ta cần chứng minh hai cạnh của nó bằng nhau.
Bước 1: Chứng minh ABEC là hình bình hành.
Ta có AB∥CD (theo giả thiết hình thang), suy ra AB∥CE (vì E nằm trên đường thẳng CD).
Ta có BE∥AC (theo cách dựng).
Một tứ giác có các cặp cạnh đối song song là hình bình hành.
Vậy, tứ giác ABEC là một hình bình hành.
Bước 2: Sử dụng tính chất hình bình hành và giả thiết.
Trong hình bình hành ABEC, các cặp cạnh đối bằng nhau. Do đó, AC=BE.
Theo giả thiết của bài toán, ta có AC=BD.
Từ AC=BE và AC=BD, suy ra BE=BD.
Bước 3: Kết luận.
Xét △BDE, ta có BE=BD.
Một tam giác có hai cạnh bằng nhau là tam giác cân.
Vậy, △BDE là tam giác cân tại B.
b) Chứng minh: △ACD=△BDC.
Ở đây, ký hiệu "=" trong hình học thường có nghĩa là đồng dạng (∼) hoặc bằng nhau (hay còn gọi là đồng nhất/trùng nhau). Tuy nhiên, trong ngữ cảnh này, ý của đề bài là △ACD đồng dạng với △BDC hoặc △ACD bằng (đồng dạng và bằng) △BDC, tức là △ACD đồng dạng và bằng △BDC hay △ACD đồng nhất với △BDC.
Để chứng minh hai tam giác bằng nhau (đồng dạng và bằng), ta cần chứng minh chúng đồng dạng theo trường hợp cạnh-góc-cạnh (SAS) hoặc cạnh-cạnh-cạnh (SSS), hoặc góc-cạnh-góc (ASA).
Bước 1: Xác định các yếu tố đã biết.
Ta có AC=BD (theo giả thiết).
Cạnh CD là cạnh chung của cả hai tam giác △ACD và △BDC.
Bước 2: Tìm mối liên hệ về góc.
Từ phần a), ta đã chứng minh △BDE là tam giác cân tại B, nên ∠BDE=∠BED.
Vì BE∥AC và đường thẳng DE (chính là CD) là đường cắt, nên ∠ACD và ∠BED là hai góc đồng vị.
Do đó, ∠ACD=∠BED.
Từ ∠BDE=∠BED và ∠ACD=∠BED, suy ra ∠BDE=∠ACD.
Góc ∠BDE chính là góc ∠BDC.
Bước 3: Kết luận.
Xét △ACD và △BDC:
AC=BD (giả thiết)
∠ACD=∠BDC (chứng minh trên)
CD là cạnh chung
Vậy, △ACD≅△BDC (theo trường hợp cạnh-góc-cạnh - SAS).
c) Chứng minh: Hình thang ABCD là hình thang cân.
Để chứng minh một hình thang là hình thang cân, ta cần chứng minh hai cạnh bên của nó bằng nhau hoặc hai góc kề một đáy bằng nhau.
Bước 1: Sử dụng kết quả từ phần b).
Từ phần b), ta đã chứng minh được △ACD≅△BDC.
Bước 2: Suy ra các cạnh tương ứng bằng nhau.
Vì hai tam giác △ACD và △BDC bằng nhau, các cạnh tương ứng của chúng cũng bằng nhau.
Cạnh AD của △ACD tương ứng với cạnh BC của △BDC.
Do đó, AD=BC.
Bước 3: Kết luận.
Hình thang ABCD có AB∥CD và hai cạnh bên AD=BC.
Theo định nghĩa, một hình thang có hai cạnh bên bằng nhau là hình thang cân.
Vậy, hình thang ABCD là hình thang cân.
-
Có: BE // AC, mà AC = BD (giả thiết)
→ BE = BD (vì BE // AC và cùng độ dài)
→ ΔBDE có BE = BD ⇒ tam giác cân tại B ✅
-
Có: AC = BD (giả thiết), CD chung
→ ΔACD = ΔBDC (theo cạnh – cạnh – cạnh) ✅
-
Hình thang có AB // CD và AC = BD
→ ABCD là hình thang cân ✅
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
107278
-
Hỏi từ APP VIETJACK67830
-
44998
-
38171


