bài 1
Cho hình bình hành ABCD, gọi K, I lần lượt là trung điểm của các cạnh AB, CD. Gọi M, N lần lượt là giao điểm của AI, CK với đường chéo BD. Chứng minh
d) AC, BD, IK đồng quy tại 1 điểm
nhanhhh ak
Quảng cáo
3 câu trả lời 762
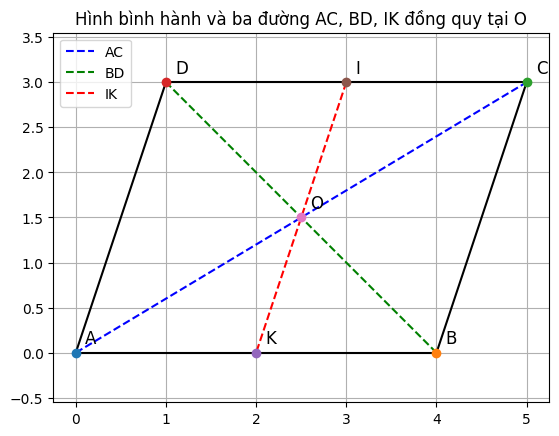
✳️ Bước 1: Gọi O là giao điểm của hai đường chéo AC và BD
Vì ABCD là hình bình hành ⇒ hai đường chéo cắt nhau tại trung điểm của mỗi đường.
⇒ O = AC ∩ BD , và O là trung điểm của cả AC và BD.
✳️ Bước 2: Xét hai điểm K và I
K là trung điểm của AB
I là trung điểm của CD
⇒ Đoạn thẳng IK là đoạn nối hai trung điểm của hai cạnh đối trong hình bình hành.
Trong hình bình hành, các cạnh đối song song và bằng nhau, nên:
AB // CD ⇒ IK // AD
Mà AD cắt hai đường chéo tại các điểm khác nhau ⇒ IK sẽ cắt đường chéo AC tại một điểm nào đó
Hãy gọi G = IK ∩ AC
Ta cần chứng minh rằng điểm G cũng nằm trên đường chéo BD ⇒ Khi đó AC, BD, IK đồng quy tại G
✳️ Bước 3: Chứng minh điểm G nằm trên đường chéo BD
Giờ ta chứng minh rằng đường thẳng IKIKIK cắt BDBDBD tại trung điểm O.
Ta làm như sau:
K là trung điểm của AB,
I là trung điểm của CD
Ta áp dụng định lý trung điểm:
Trong tam giác, đường nối hai trung điểm của hai cạnh thì song song và bằng nửa cạnh thứ ba.
Áp dụng vào tam giác ABC, K là trung điểm AB, còn O là trung điểm AC
⇒ Đoạn nối KO sẽ song song và bằng nửa cạnh BC
Tương tự, xét tam giác DCA, điểm I là trung điểm CD, O là trung điểm AC ⇒ đoạn IO song song và bằng nửa cạnh DA
⇒ Vậy thì cả hai đoạn IO và KO đều nằm trên đường IK
→ Suy ra: Điểm O nằm trên đoạn thẳng IK
✅ Kết luận:
AC và BD cắt nhau tại O
IK cũng đi qua O
⇒ 3 đường thẳng AC, BD, và IK đồng quy tại điểm O
Vì K, I lần lượt là trung điểm của AB, CD nên AK = 1/2 AB và CI = 1/2 CD. Mà AB = CD (do ABCD là hình bình hành) nên AK = CI. Xét tứ giác AKCI có: AK // CI (do AB // CD) AK = CI (chứng minh trên) => AKCI là hình bình hành. => AC và KI cắt nhau tại trung điểm của mỗi đường. Mà O là trung điểm của AC nên O cũng là trung điểm của KI. => O ∈ IK hay IK đi qua O.
Vậy AC, BD, IK đồng quy tại O.
1. Xét hình bình hành ABCD:
Gọi O là giao điểm của hai đường chéo AC và BD.
Trong hình bình hành, hai đường chéo cắt nhau tại trung điểm của mỗi đường, nên O là trung điểm của AC và BD.
2. Xét tứ giác AKCI:
Ta có AK song song với IC (vì AB song song với CD).
K là trung điểm của AB, I là trung điểm của CD, và AB = CD (tính chất hình bình hành). Do đó, AK = IC.
Vì AK song song và bằng IC, nên tứ giác AKCI là hình bình hành.
3. Xét đường chéo AI và CK của hình bình hành AKCI:
Trong hình bình hành AKCI, hai đường chéo AI và CK cắt nhau tại trung điểm của mỗi đường.
Gọi P là giao điểm của AI và CK. P là trung điểm của AI và CK.
4. Xét tam giác ABD:
K là trung điểm của AB.
O là trung điểm của BD.
Do đó, KO là đường trung bình của tam giác ABD. Suy ra KO song song với AD.
5. Xét tam giác BCD:
I là trung điểm của CD.
O là trung điểm của BD.
Do đó, IO là đường trung bình của tam giác BCD. Suy ra IO song song với BC.
6. Kết luận:
Ta có O là trung điểm của BD.
IK là đường nối trung điểm của AB và CD.
Trong hình bình hành AKCI, IK là đường chéo.
Vì AKCI là hình bình hành, O là trung điểm của BD.
Ta thấy AC, BD, IK đều đi qua điểm O (O là trung điểm của AC và BD; và O cũng là trung điểm của IK trong hình bình hành AKCI).
Vậy AC, BD, IK đồng quy tại điểm O.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107593
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68300
Đã trả lời bởi chuyên gia
68300 -
 Đã trả lời bởi chuyên gia
52884
Đã trả lời bởi chuyên gia
52884 -
 Đã trả lời bởi chuyên gia
47390
Đã trả lời bởi chuyên gia
47390 -
 Đã trả lời bởi chuyên gia
45461
Đã trả lời bởi chuyên gia
45461 -
 Đã trả lời bởi chuyên gia
45109
Đã trả lời bởi chuyên gia
45109 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38488
Đã trả lời bởi chuyên gia
38488 -
 Đã trả lời bởi chuyên gia
38230
Đã trả lời bởi chuyên gia
38230


