Quảng cáo
4 câu trả lời 204
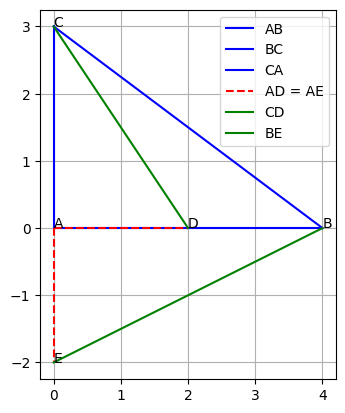
Tam giác ABC vuông tại A cho biết AC ⊥ AB.
Điểm E nằm trên tia đối của AC với AE = AD làm tam giác AED vuông cân tại A.
Do đó, AD ⊥ AE và góc = 90∘.
Từ đó, AD // AC khiến CD theo hướng tương tự AC, và AE // AB khiến BEBEBE theo hướng tương tự AB.
ây là một bài toán hình học thú vị. Để chứng minh CD vuông góc với BE, chúng ta sẽ sử dụng phương pháp chứng minh hai tam giác bằng nhau và các tính chất về góc.
Lưu ý quan trọng: Với đề bài như bạn cung cấp, kết luận "CD vuông góc với BE" chỉ đúng khi tam giác ABC không chỉ vuông tại A mà còn là tam giác vuông cân tại A (tức là AB = AC). Nếu không có điều kiện AB = AC, thì CD và BE không nhất thiết phải vuông góc với nhau.
Tôi sẽ giải bài toán này với giả định rằng đề bài có thể ngầm định hoặc thiếu điều kiện AB = AC để kết quả chứng minh là đúng.
Chứng minh:
Xác định các góc vuông tại A:
Tam giác ABC vuông tại A, nên BAC =90∘.
Điểm D nằm trên cạnh AB.
Điểm E nằm trên tia đối của tia AC. Điều này có nghĩa là ba điểm E, A, C thẳng hàng và A nằm giữa E và C.
Do đó, đường thẳng AE vuông góc với đường thẳng AB. Hay EAB =90∘.
Tương tự, DAC =90∘.
Chứng minh △ABE=△ADC:
Xét △ABE và △ADC có:
AE=AD (giả thiết).
EAB =DAC =90∘ (chứng minh ở bước 1).
AB=AC (Điều kiện này phải có để chứng minh được. Chúng ta đang giả định điều kiện này được ngầm định hoặc thiếu trong đề bài để lời giải có thể thực hiện được).
Vậy, △ABE=△ADC (cạnh - góc - cạnh: c.g.c).
Suy ra các góc tương ứng bằng nhau:
Từ △ABE=△ADC (chứng minh ở bước 2), suy ra:
ABE =ADC (hai góc tương ứng). (1)
AEB =ACD (hai góc tương ứng). (2)
Chứng minh CD vuông góc với BE:
Gọi I là giao điểm của BE và CD.
Xét tam giác ABE vuông tại A. Tổng hai góc nhọn trong tam giác vuông bằng 90∘.
ABE +AEB =90∘. (3)
Từ (1), ta có ABE =ADC .
Từ (2), ta có AEB =ACD .
Thay ABE bằng ADC và AEB bằng ACD vào (3):
ADC +ACD =90∘. (4)
Bây giờ, xét tam giác IDC (là tam giác chứa giao điểm I của CD và BE).
Tổng ba góc trong tam giác IDC là 180∘:
DIC +IDC +ICD =180∘.
IDC chính là ADC .
ICD chính là ACD .
Vậy, DIC +(ADC +ACD )=180∘.
Từ (4), ta biết (ADC +ACD )=90∘.
Thay vào biểu thức trên:
DIC +90∘=180∘.
DIC =180∘−90∘=90∘.
Góc DIC =90∘ có nghĩa là đường thẳng CD vuông góc với đường thẳng BE.
Kết luận:
Vậy, CD vuông góc với BE.
Lưu ý quan trọng thêm một lần nữa: Chứng minh này chỉ đúng nếu △ABC là tam giác vuông cân tại A (tức AB=AC). Nếu đề bài gốc của bạn không có điều kiện này, thì có thể đề bài bị thiếu hoặc là một bài toán nâng cao hơn yêu cầu sử dụng kiến thức khác (mà thường thì không phải ở mức độ này nếu nó không vuông cân).
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
107278
-
Hỏi từ APP VIETJACK67830
-
44998
-
38171


