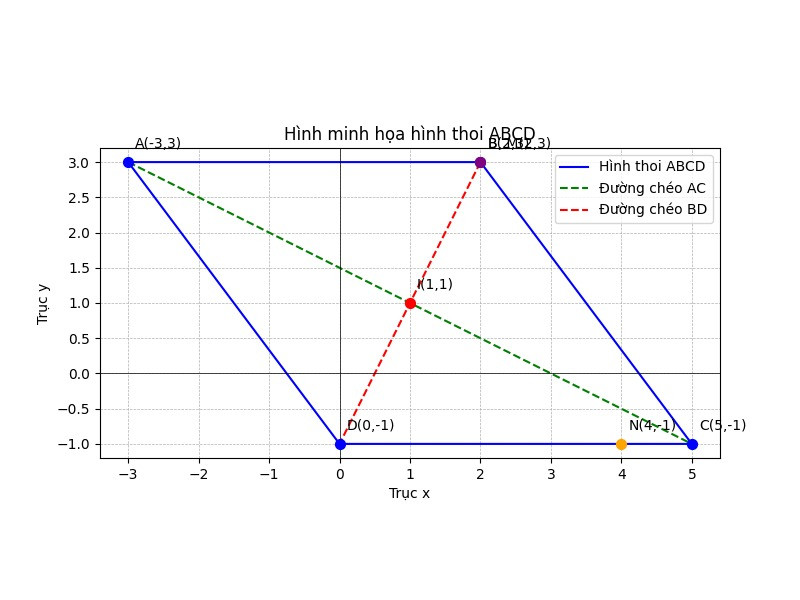
$I(1, 1)$ là tâm đối xứng. $N(4, -1) \in CD$.
 Lấy đối xứng $N$ qua $I$ được $N' = (2 \cdot 1 - 4, 2 \cdot 1 - (-1)) = (-2, 3)$.
 $N \in CD \Rightarrow N' \in AB$.
 $AB$ đi qua $M(2, 3)$ và $N'(-2, 3) \Rightarrow$ Phương trình $AB: y - 3 = 0$.
 $CD$ song song $AB$ và đi qua $N(4, -1) \Rightarrow$ Phương trình $CD: y + 1 = 0$.

 $h = d(I, AB) = \frac{|1 - 3|}{\sqrt{0^2 + 1^2}} = 2$.
 $AC = 2BD \Rightarrow IA = 2IB$.
 $\triangle IAB$ vuông tại $I$: $\frac{1}{h^2} = \frac{1}{IA^2} + \frac{1}{IB^2}$.
 $\frac{1}{4} = \frac{1}{(2IB)^2} + \frac{1}{IB^2} = \frac{5}{4IB^2} \Rightarrow IB^2 = 5$.
 $IA^2 = 4 \cdot IB^2 = 20$.

 $A(x_A, 3), B(x_B, 3)$.
 $C(2-x_A, -1), D(2-x_B, -1)$.
 $IA^2 = (x_A-1)^2 + (3-1)^2 = 20 \Rightarrow (x_A-1)^2 = 16 \Rightarrow x_A-1 = \pm 4$.
$\Rightarrow x_A = 5$ hoặc $x_A = -3$.
 $IB^2 = (x_B-1)^2 + (3-1)^2 = 5 \Rightarrow (x_B-1)^2 = 1 \Rightarrow x_B-1 = \pm 1$.
$\Rightarrow x_B = 2$ hoặc $x_B = 0$.
 $AC \perp BD \Rightarrow \vec{AC} \cdot \vec{BD} = 0 \Rightarrow (2-2x_A)(2-2x_B) + 16 = 0 \Rightarrow (1-x_A)(1-x_B) = -4$.
 Nếu $x_A = -3 \Rightarrow (1 - (-3))(1-x_B) = -4 \Rightarrow 4(1-x_B) = -4 \Rightarrow x_B = 2$.
 Nếu $x_A = 5 \Rightarrow (1 - 5)(1-x_B) = -4 \Rightarrow -4(1-x_B) = -4 \Rightarrow x_B = 0$.

Trường hợp 1: $A(-3, 3), B(2, 3) \Rightarrow C(5, -1), D(0, -1)$.
 $M(2, 3)$ thuộc đoạn $AB$.
 $N(4, -1)$ thuộc đoạn $CD$ (vì $0 \le 4 \le 5$).
 Nhận.

Trường hợp 2: $A(5, 3), B(0, 3) \Rightarrow C(-3, -1), D(2, -1)$.
 $M(2, 3)$ thuộc đoạn $AB$.
 $N(4, -1)$ không thuộc đoạn $CD$.
 Loại.

vậy

$A(-3, 3)$, $B(2, 3)$, $C(5, -1)$, $D(0, -1)$.