Quảng cáo
2 câu trả lời 140
Để xác định mặt phẳng nào song song với mặt phẳng \( MNO \) trong hình chóp \( SABCD \) với đáy \( ABCD \) là hình bình hành, chúng ta tiến hành như sau:
### 1. Xác định các điểm:
- Let \( S \) là đỉnh chóp.
- Let \( A, B, C, D \) là các đỉnh của hình bình hành, với \( O \) là tâm của hình bình hành đó.
- \( M \) là trung điểm của \( SA \).
- \( N \) là trung điểm của \( SD \).
### 2. Xác định mặt phẳng \( MNO \):
- Vì \( M \) và \( N \) là những trung điểm, nên \( MN \) sẽ nằm trong mặt phẳng đi qua \( S \) và hai điểm \( A \) và \( D \).
- Mặt phẳng \( MNO \) chứa các điểm \( M, N \) và \( O \).
### 3. Tính chất của mặt phẳng song song:
Để xác định mặt phẳng nào song song với \( MNO \), ta cần một mặt phẳng chứa một đường thẳng song song với \( MN \) và qua \( O \).
### 4. Lập mặt phẳng song song:
1. **Mặt phẳng chứa \( O \)**: Mặt phẳng qua \( O \) và song song với \( MR \) (tiếp điểm của đường thẳng nối \( M \) và các điểm trong đáy) có thể được xác định.
2. **Bất kỳ mặt phẳng nào đi qua \( O \)** và chứa đường thẳng song song với dây MN cũng sẽ là mặt phẳng song song với \( MNO \).
### Kết luận:
Mặt phẳng đi qua điểm \( O \) và chứa các đường thẳng song song với \( MN \) từ các điểm A, B, C, D sẽ là mặt phẳng song song với mặt phẳng \( MNO \).
Một ví dụ có thể là mặt phẳng đi qua \( O \) và song song với mặt phẳng đáy \( ABCD \). Tóm lại, mọi mặt phẳng chứa \( O \) và song song với \( SA \) hoặc \( SD \) đều là mặt phẳng song song với \( MNO \).
Ta có: $M, O$ lần lượt là trung điểm của $SA, AC$
$\Rightarrow MO$ là đường trung bình của $\triangle SAC$
$\Rightarrow MO // SC$
$\Rightarrow MO // (SBC)$
Ta có: $N, O$ lần lượt là trung điểm của $SD, BD$
$\Rightarrow NO$ là đường trung bình của $\triangle SBD$
$\Rightarrow NO // SB$
$\Rightarrow NO // (SBC)$
Mà $MO \cap NO = O$ trong $(MNO)$
$\Rightarrow (SBC) // (MNO)$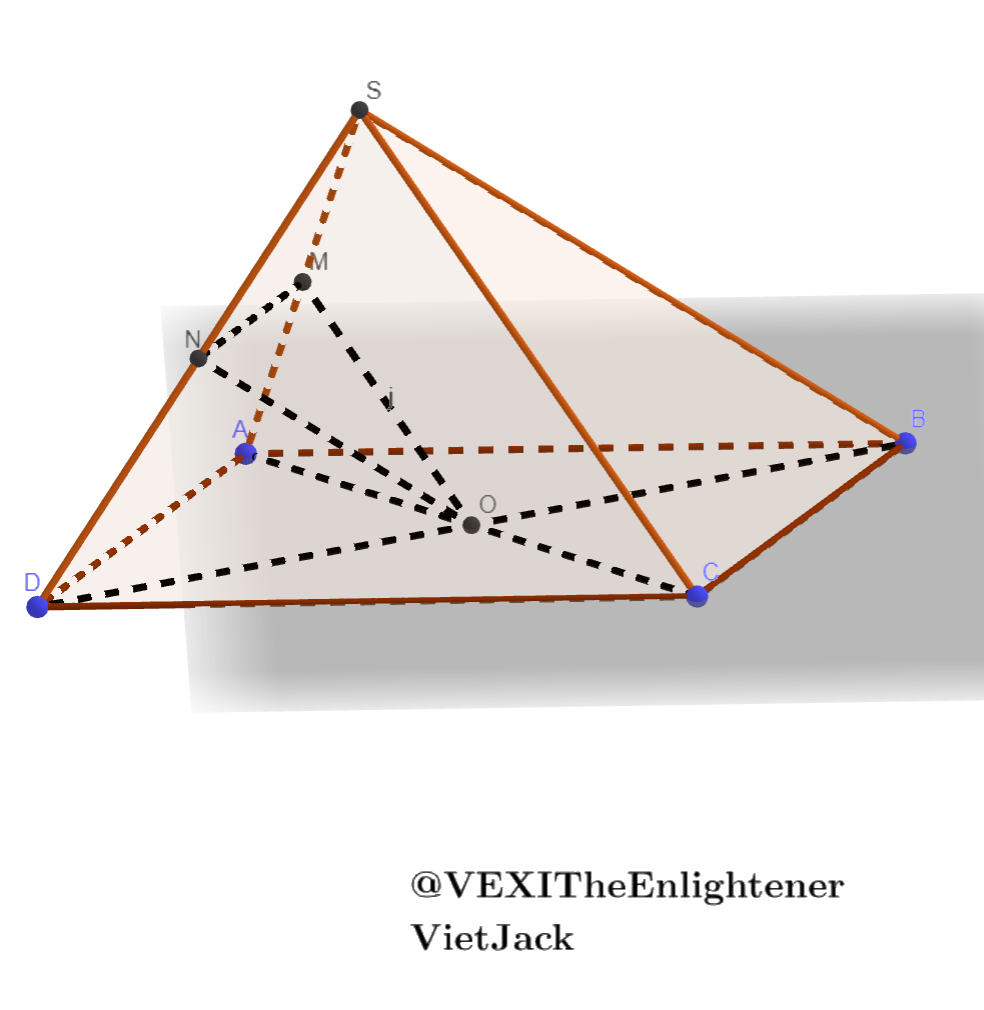
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129637
Đã trả lời bởi chuyên gia
129637 -
 Đã trả lời bởi chuyên gia
104061
Đã trả lời bởi chuyên gia
104061 -
 Đã trả lời bởi chuyên gia
94054
Đã trả lời bởi chuyên gia
94054 -
 Đã trả lời bởi chuyên gia
69272
Đã trả lời bởi chuyên gia
69272



