Question

Đã trả lời bởi chuyên gia

Answer 1

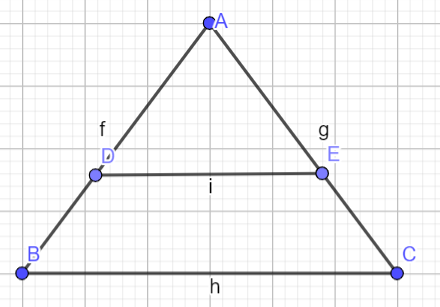
Hỏi đáp VietJack

Tam giác ABC cân tại A nên

$\hat{A B C} = \hat{A C B} m à \hat{A B C} + \hat{A C B} = 180^{0} - \hat{B A C} (t í n h c h ấ t 3 g ó c t r o n g 1 t a m g i á c) \Rightarrow 2 . \hat{A B C} = 180^{o} - \hat{B A C}$
Ta lại có AD=AE nên tam giác ADE cân tại A

$\hat{A D E} = \hat{A E D} m à \hat{A D E} + \hat{A E D} = 180^{0} - \hat{D A E} \Rightarrow 2 \hat{A D E} = 180^{0} - \hat{D A E}$

do đó

$\hat{A B C} = \hat{A D E}$

mà 2 góc này nằm ở vị trí đồng vị nên DE// BC

Xét tứ giác BDEC có

DE// BC

\hat{A B C} = \hat{A C B}

tứ giác BDEC là hình thang cân .

b. Tam giác ABC cân tại A . góc a =70^o

^{$\hat{B} = \hat{C} = \frac{(180^{0} - 70^{0})}{2} = 55^{0}$}

ta có

\hat{B} = \hat{A D E} = 55^{0} (2 g ó c đ ồ n g v ị) m à \hat{A D E} + \hat{E D B} = 180^{0} \Rightarrow \hat{E D B} = 180^{0} - \hat{A D E} = 180^{0} - 55^{0} = 125^{o}

Tương tự ta có

\hat{D E C} = 125^{0}

...Xem thêm

Answer 2

Hỏi đáp VietJack

Tam giác ABC cân tại A nên

$\hat{A B C} = \hat{A C B} m à \hat{A B C} + \hat{A C B} = 180^{0} - \hat{B A C} (t í n h c h ấ t 3 g ó c t r o n g 1 t a m g i á c) \Rightarrow 2 . \hat{A B C} = 180^{o} - \hat{B A C}$
Ta lại có AD=AE nên tam giác ADE cân tại A

$\hat{A D E} = \hat{A E D} m à \hat{A D E} + \hat{A E D} = 180^{0} - \hat{D A E} \Rightarrow 2 \hat{A D E} = 180^{0} - \hat{D A E}$

do đó

$\hat{A B C} = \hat{A D E}$

mà 2 góc này nằm ở vị trí đồng vị nên DE// BC

Xét tứ giác BDEC có

DE// BC

\hat{A B C} = \hat{A C B}

tứ giác BDEC là hình thang cân .

b. Tam giác ABC cân tại A . góc a =70^o

^{$\hat{B} = \hat{C} = \frac{(180^{0} - 70^{0})}{2} = 55^{0}$}

ta có

\hat{B} = \hat{A D E} = 55^{0} (2 g ó c đ ồ n g v ị) m à \hat{A D E} + \hat{E D B} = 180^{0} \Rightarrow \hat{E D B} = 180^{0} - \hat{A D E} = 180^{0} - 55^{0} = 125^{o}

Tương tự ta có

\hat{D E C} = 125^{0}

Answer 3

### **a) Chứng minh BDEC là hình thang cân**

**Hình vẽ:**
- Vẽ tam giác cân $ ABC $ với $ AB = AC $, $ \widehat{A} = 70^\circ $.
- Lấy điểm $ D $ trên $ AB $ và điểm $ E $ trên $ AC $ sao cho $ AD = AE $.

**Chứng minh:**
1. **Tam giác $ ADE $ cân tại $ A $:**
- Vì $ AD = AE $ (giả thiết), nên $ \triangle ADE $ cân tại $ A $.
- Suy ra $ \widehat{ADE} = \widehat{AED} $.

2. **Tính góc $ \widehat{ADE} $:**
- Trong $ \triangle ADE $, ta có:
\[
\widehat{ADE} = \widehat{AED} = \frac{180^\circ - \widehat{A}}{2} = \frac{180^\circ - 70^\circ}{2} = 55^\circ.
\]

3. **Chứng minh $ DE \parallel BC $:**
- Ta có $ \widehat{ADE} = \widehat{ABC} = 55^\circ $ (vì $ \triangle ABC $ cân tại $ A $ nên $ \widehat{ABC} = \widehat{ACB} = \frac{180^\circ - 70^\circ}{2} = 55^\circ $).
- Vì $ \widehat{ADE} $ và $ \widehat{ABC} $ ở vị trí đồng vị và bằng nhau, nên $ DE \parallel BC $.

4. **Kết luận $ BDEC $ là hình thang cân:**
- Tứ giác $ BDEC $ có $ DE \parallel BC $ (chứng minh trên) và $ \widehat{B} = \widehat{C} = 55^\circ $ (do $ \triangle ABC $ cân tại $ A $).
- Vậy $ BDEC $ là hình thang cân (vì có hai cạnh đáy song song và hai góc kề một đáy bằng nhau).

### **b) Tính các góc của hình thang cân $ BDEC $**

**Biết $ \widehat{A} = 70^\circ $, ta đã có:**
- $ \widehat{B} = \widehat{C} = 55^\circ $ (tính chất tam giác cân $ ABC $).

**Tính góc $ \widehat{BDE} $ và $ \widehat{CED} $:**
- Vì $ BDEC $ là hình thang cân nên:
- $ \widehat{BDE} = \widehat{CED} $.
- Trong hình thang cân, tổng hai góc kề một cạnh bên bằng $ 180^\circ $:
\[
\widehat{B} + \widehat{BDE} = 180^\circ \implies 55^\circ + \widehat{BDE} = 180^\circ \implies \widehat{BDE} = 125^\circ.
\]
Tương tự, $ \widehat{CED} = 125^\circ $.

**Kết quả:**
- Các góc của hình thang cân $ BDEC $ là:
- $ \widehat{B} = \widehat{C} = 55^\circ $,
- $ \widehat{BDE} = \widehat{CED} = 125^\circ $.

### **Tóm tắt đáp án:**
a) **Chứng minh $ BDEC $ là hình thang cân:**
- $ DE \parallel BC $ và $ \widehat{B} = \widehat{C} $, suy ra $ BDEC $ là hình thang cân.

b) **Các góc của hình thang cân $ BDEC $:**
- $ \widehat{B} = \widehat{C} = 55^\circ $,
- $ \widehat{BDE} = \widehat{CED} = 125^\circ $.