Cho tam giác ABC,đường thẳng d // BC cắt AB và AC và trung tuyến AM theo thứ tự Là E,F,N. Trên tia đối của tia FB lấy điểm K, đường thẳng KN cắt AB tại P đường thẳng KM cắt AC tại Q. Chứng minh PQ//BC
Quảng cáo
1 câu trả lời 387
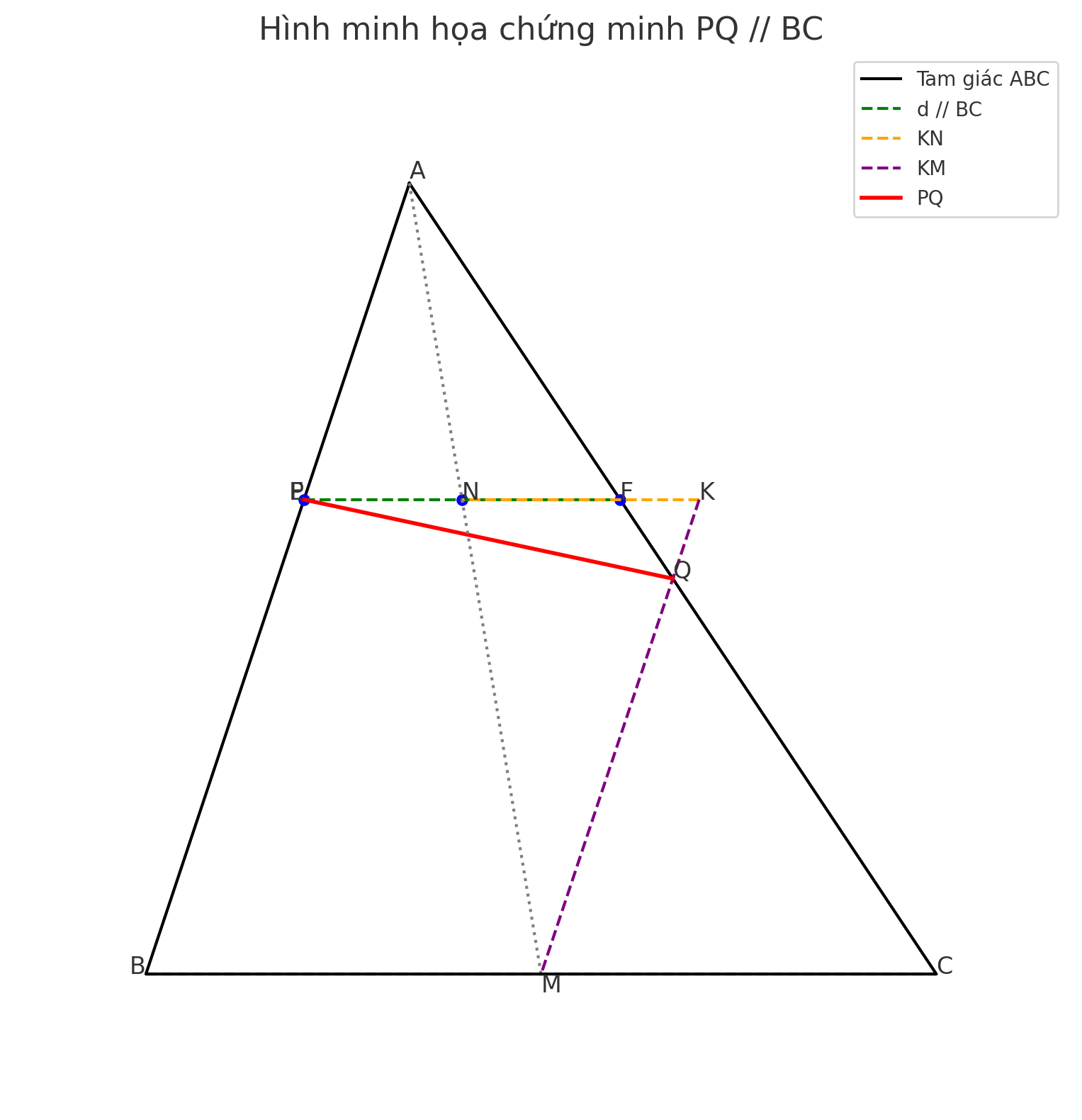
Vì MM là trung điểm của BC, nên AM là trung tuyến của △ABC.
Đường thẳng d∥BC cắt AB,AC,AM lần lượt tại E,F,N nên:
-
E∈AB
-
F∈AC
-
N∈AM
Vì d∥BC, theo định lý ta-lét thuận ta có:
Tức là E,F chia các đoạn AB,AC theo cùng tỉ lệ.
Ta biết N∈AM∩d, mà d∥BC, nên đường thẳng d cắt trung tuyến AM tại điểm N và tạo ra tam giác nhỏ AEF đồng dạng với tam giác ABC.
Từ đó, các đoạn:
-
AE,EB
-
AF,FC
-
AN,NM
Chia theo cùng tỉ lệ:
Xét tam giác △AFK, có:
-
F∈AC
-
K∈ tia đối của FB ⇒ ba điểm F,B,K thẳng hàng theo thứ tự K−F−B
-
N∈AF
-
M∈AK
-
Đường thẳng KN cắt AB tại P
-
Đường thẳng KM cắt AC tại Q
Từ hình vẽ và các điều kiện:
⇒ Theo định lý đồng tỉ số, khi các đoạn thẳng chia các cạnh của tam giác theo cùng tỉ số, thì đoạn nối các điểm chia đó song song với cạnh thứ ba.
⇒ PQ∥BC
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107437
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68061
Đã trả lời bởi chuyên gia
68061 -
 Đã trả lời bởi chuyên gia
52846
Đã trả lời bởi chuyên gia
52846 -
 Đã trả lời bởi chuyên gia
47344
Đã trả lời bởi chuyên gia
47344 -
 Đã trả lời bởi chuyên gia
45400
Đã trả lời bởi chuyên gia
45400 -
 Đã trả lời bởi chuyên gia
45045
Đã trả lời bởi chuyên gia
45045 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38412
Đã trả lời bởi chuyên gia
38412 -
 Đã trả lời bởi chuyên gia
38191
Đã trả lời bởi chuyên gia
38191
Gửi báo cáo thành công!


