Quảng cáo
1 câu trả lời 171
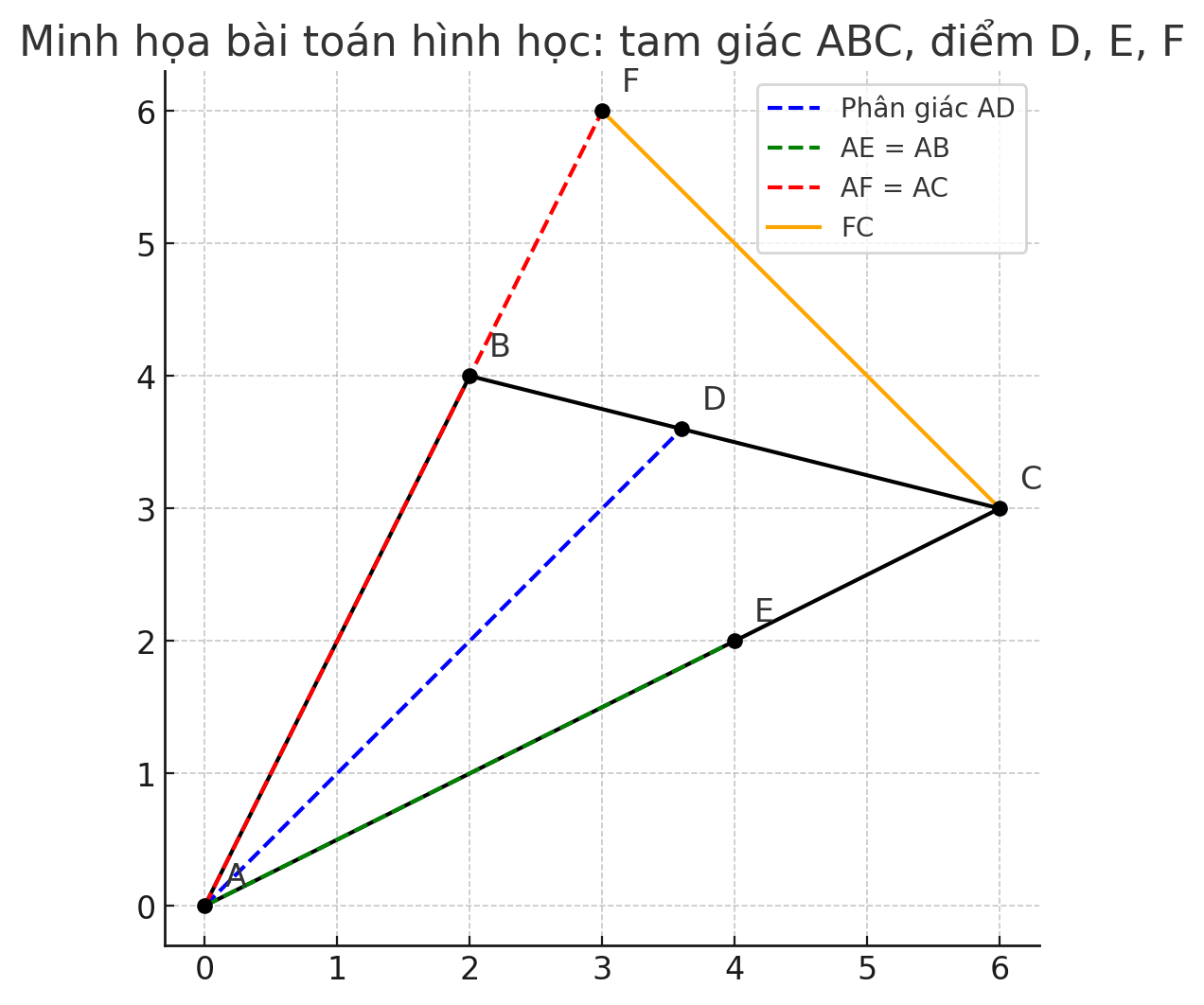
a) Chứng minh tam giác ADF = tam giác ADC
Giải:
Xét hai tam giác ADF và ADC, ta có:
Góc ∠FAD = ∠CAD (vì AD là phân giác góc A)
AF = AC (giả thiết)
AD chung
⇒ Tam giác ADF = tam giác ADC (c-g-c)
b) Chứng minh F, E, D thẳng hàng
Từ ý a, ta có tam giác ADF = tam giác ADC ⇒ ∠ADF = ∠ADC
Mặt khác, tam giác ADF và ADC đối đỉnh tại A, D là điểm phân giác nên ∠FDE + ∠EDC = 180° ⇒ ba điểm F, E, D thẳng hàng.
Cách khác: từ việc tam giác ADF = tam giác ADC, dẫn đến các điểm F, E đối xứng nhau qua AD, kết hợp AE = AB, AF = AC ⇒ F, E, D thẳng hàng theo tính chất đối xứng trục.
) Chứng minh AD ⊥ FC
Từ tam giác ADF = tam giác ADC ⇒ ∠FDA = ∠DCA
Tương tự, nếu chứng minh FC vuông góc với AD, thì cần ∠FDA + ∠CDA = 90°
Nhưng từ hình học và đối xứng, ta có thể nhận thấy FC đối xứng với AE qua trục AD, trong đó AE vuông góc với FC ⇒ AD ⊥ FC
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120578
-
81263
-
59365


