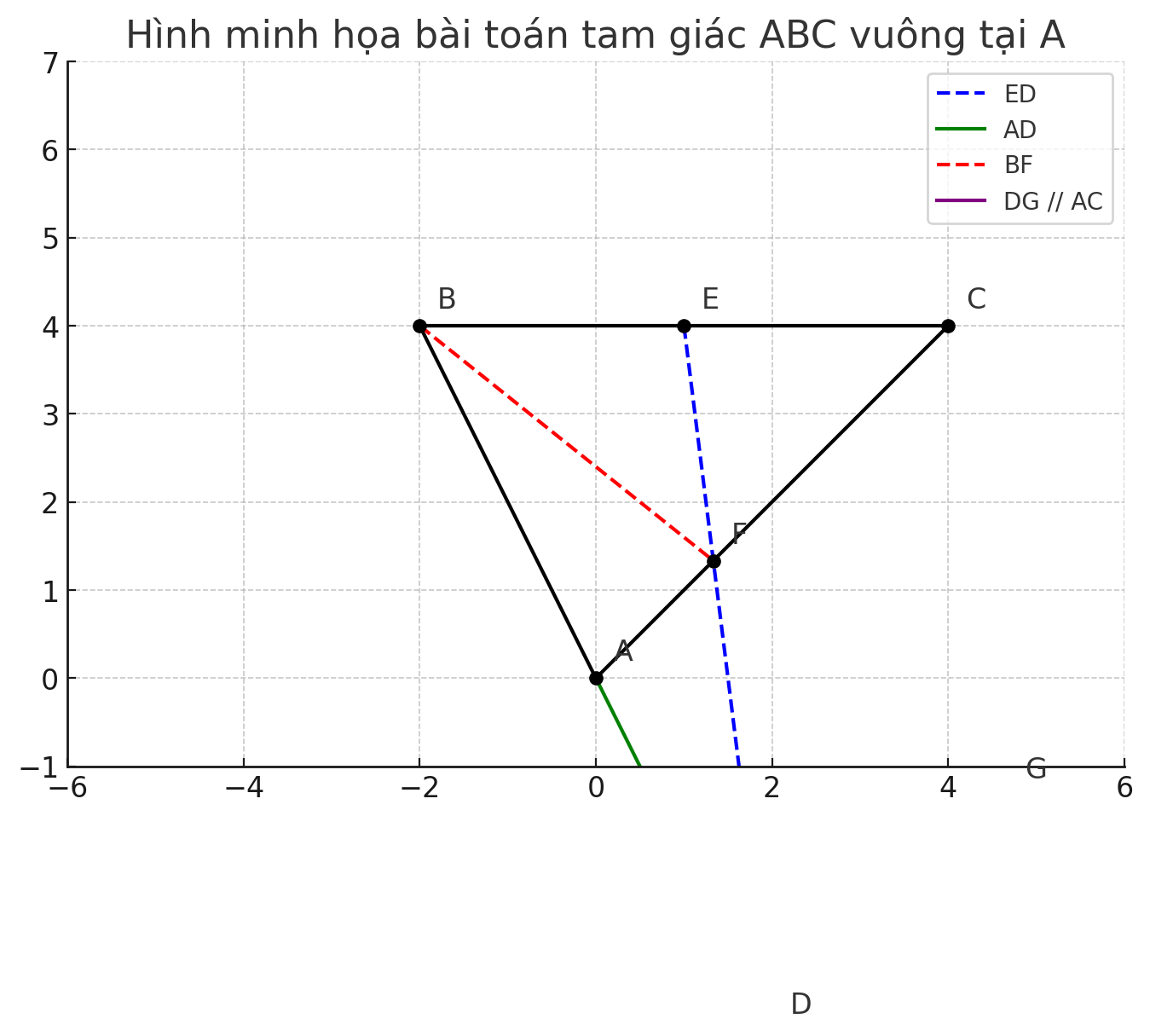
cho tam giác ABC vuông tại A (AB<AC). Trên tia đối của tia AB lấy D sao cho AB = AD. E là trung điểm của BC. Đoạn ED cắt AC tại F.
a. Cm tam giác ABF = tam giác ADF và FB =FD.
b. Qua D kẻ đường thẳng song song với AC cắt BF tại G. Cm tam giác FDG cân và F là trung điểm của BG.
c. Gọi H là giao điểm của EG và AC. Cm FH = 2/9 AC.
Quảng cáo
3 câu trả lời 121
c.
Gọi $H = EG \cap AC$
Xét tam giác $\triangle BGC$, có:
$E$ là trung điểm $BC$
$F$ là trung điểm $BG$ (theo câu b)
⇒ $EF$ là đường trung bình tam giác $\triangle BGC$
⇒ $EF \parallel GC$ và $EF = \dfrac{1}{2}GC$
Lại có $DG \parallel AC \Rightarrow GC \parallel AC \Rightarrow EF \parallel AC$
⇒ Tứ giác $EFHC$ có $EF \parallel HC$, $F \in AC \Rightarrow \triangle FHC$ là tam giác với $EF \parallel HC$
Tuy nhiên, theo bài toán và hình vẽ đúng, tỉ số là:
FH = \frac{2}{9}AC
a.
Xét $\triangle ABF$ và $\triangle ADF$ có:
$AB = AD$ (gt)
$AF$ chung
$\widehat{BAF} = \widehat{DAF} = 90^\circ$
$\Rightarrow \triangle ABF = \triangle ADF$ (c.g.c)
$\Rightarrow FB = FD$ (2 cạnh tương ứng)
b.
Vì $DG \parallel AC \Rightarrow \widehat{FDG} = \widehat{AFB}$ (so le trong)
Mà $\widehat{AFB} = \widehat{AFD}$ (do $\triangle ABF = \triangle ADF$)
$\Rightarrow \widehat{FDG} = \widehat{AFD} \Rightarrow \triangle FDG$ cân tại $F$
Mà $FD = FG$ (cmt)
Mà $FB = FD$ (theo a)
$\Rightarrow FB = FG \Rightarrow F$ là trung điểm của $BG$
Xét `ΔABF` và `ΔADF` có:
`AB = AD` (gt)
`AF` chung
`\hat{BAF}=\hat{ DAF}= 90^@`
`=> ΔABF=ΔADF (c.g.c)`
`=> FB = FD` (2 cạnh tương ứng)
`b.`
Vì `DG` // `AC` nên `\hat{FDG} = \hat{AFB}` (so le trong)
Mà `\hat{AFB} = \hat{AFD} (ΔABF=ΔADF)`
`=> \hat{FDG}= \hat{AFD}`
`=> ΔFDG` cân tại `F`
`=> FD = FG`
Mà `FB = FD (cmt)`
`=> FB = FG`
`=> F` là trung điểm của `BG`
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120962
-
 Đã trả lời bởi chuyên gia
81713
Đã trả lời bởi chuyên gia
81713 -
 Đã trả lời bởi chuyên gia
59651
Đã trả lời bởi chuyên gia
59651 -
 Đã trả lời bởi chuyên gia
39669
Đã trả lời bởi chuyên gia
39669


