Cho tam giác ABC cân tại A, lấy M là trung điểm của cạnh BC.
1) Chứng minh: tam giác ABM = tam giác ACM.
2) Vẽ CN vuông góc với AB tại N. Đường thẳng AM và CN cắt nhau tại L. Chứng minh rằng BL vuông góc với AC
Quảng cáo
2 câu trả lời 200
Xét hai tam giác ABM và ACM, ta có:
AB = AC (giả thiết tam giác cân tại A)
MB = MC (do M là trung điểm BC)
AM = AM (cạnh chung)
Theo trường hợp cạnh – cạnh – cạnh (c.g.c):
2) Vẽ CN vuông góc AB tại N, CN cắt AM tại L. Chứng minh: BL ⊥ AC
Dùng tính chất hình học và tam giác bằng nhau
Từ (1): Tam giác ABM = ACM
⇒ ∠ABM = ∠ACM
Xét hai tam giác vuông CNL và BNL:
Do CN ⊥ AB nên ∠CNA = 90°
⇒ Tam giác CNL vuông tại N
Tương tự, ta sẽ chứng minh rằng ∠BLM = 90°, tức là BL ⊥ AC
→ Ta cần chứng minh tam giác BLC vuông tại L nếu được.
AM là trung tuyến từ A ⇒ chia tam giác ABC thành 2 phần có diện tích bằng nhau.
CN ⊥ AB, L là giao điểm CN và AM
Khi đó, điểm L là trực tâm tam giác ABC (do CN và AM là 2 đường cao)
Mà rong tam giác có trực tâm, đường nối từ đỉnh còn lại đến trực tâm vuông góc với cạnh đối.
Vì L là trực tâm tam giác ABC ⇒ BL ⊥ AC
> BL ⊥ AC vì L là trực tâm của tam giác ABC.
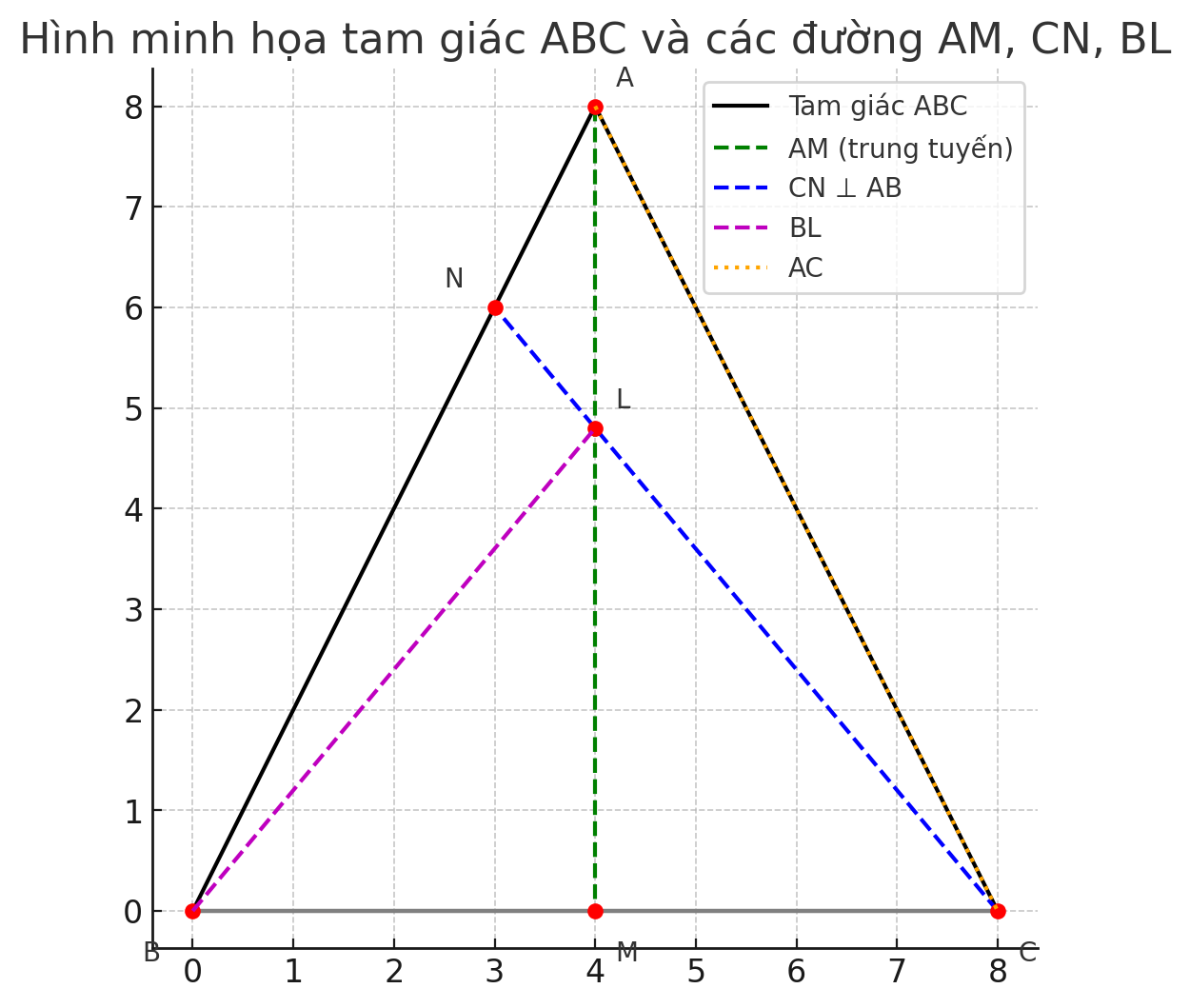
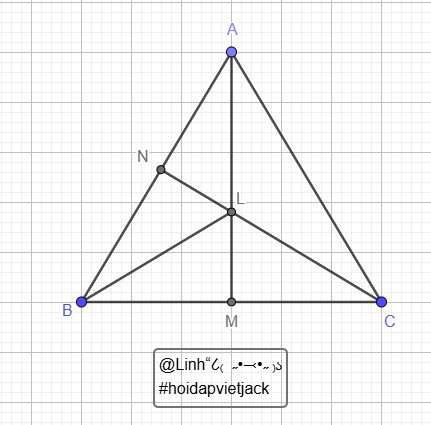
Xét `ΔABM` và `ΔACM` có:
`AB = AC` (do `ΔABC` cân tại `A`)
`AM` là cạnh chung
`=> ΔABM = ΔACM (c.c.c)`
`b)`
Ta có:
`AM` là đường trung tuyến của `ΔABC` và `ΔABC` cân tại `A` nên
`=> AM` cũng là đường cao `=> AM ⊥ BC.`
Xét `ΔABC` có:
`AM ⊥ BC`
`CN ⊥ AB`
`AM` cắt `CN` tại `L`
`=> L` là trực tâm của `ΔABC`
`=> BL ⊥ AC`
Quảng cáo
Bạn hỏi - Chuyên gia trả lời
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Đã trả lời bởi chuyên gia
7808 -
Đã trả lời bởi chuyên gia
7313
-
Đã trả lời bởi chuyên gia
6304
-
보고 싶어요
2510 điểm
-
🐟祖尼⚡
1195 điểm
-
nhỏ na
1100 điểm
-
`color{blue}text{HuyTùng☢`
1010 điểm
-
언니, 사랑해😗
965 điểm
-
౨ৎ𝘉ắ𝘱ت𝘭𝘶ộ𝘤تđê⋅˚₊‧ ଳ⋆.࿔*:･🌽
630 điểm
-
Ben 10K
595 điểm
-
𝘳𝘺𝘯.𝘭𝘦𝘦ッ
545 điểm
-
devestro
520 điểm
-
Kiều Anh 450 điểm
-
pp mn, từ nay off
400 điểm
-
jgdmaX
345 điểm
-
너 없는 파리
340 điểm
-
Vợ Jungwon Bồ Jay
265 điểm
-
🌸˚˖𓍢ִ໋🌷͙֒✧ᕼàᑎᕼ.丅ᖇᗩᑎǤ.丅ᖇᎥ.丅ᕼứᑕ🩷˚⋆
245 điểm
Rút gọn
Bài viết mới nhất Lớp 7
-
2 năm trước4947
