ABCD). Gọi AE, AF lần lượt là đường cao của các tam giác SAB và SAD ; góc giữa cạnh bên SB và mặt phẳng
(SAD) bằng 60°
a) Chứng minh SC L (AEF).
b) Tính thể tích khối chóp SABCD.
Quảng cáo
1 câu trả lời 154
Giả thiết:
ABCD là hình vuông cạnh $2a$
SA ⊥ mặt phẳng (ABCD)
AE ⊥ SB trong tam giác SAB, AF ⊥ SD trong tam giác SAD ⇒ $AE, AF$ là đường cao
Góc giữa SB và mặt phẳng (SAD) là $60^\circ$
a) Chứng minh SC ⊥ (AEF)
Do:
AE ⊥ SB (tam giác SAB)
AF ⊥ SD (tam giác SAD)
⇒ Mặt phẳng (AEF) ⊥ mặt phẳng (SBD), vì (AEF) chứa 2 đường cao lần lượt vuông góc SB và SD
Gọi $C \in (ABCD)$, cạnh đáy vuông ⇒ SD và SB nằm trong đáy
Ta có:
SA ⊥ đáy ⇒ SA ⊥ SB và SA ⊥ SD
SC nằm trong mặt phẳng (SBD)
Mà (AEF) ⊥ (SBD) ⇒ SC ⊥ (AEF)
b) Tính thể tích khối chóp SABCD
V diện tích đáy chiều cao
Đáy ABCD là hình vuông cạnh $2a$ ⇒ diện tích đáy:
SA ⊥ đáy ⇒ SA là chiều cao
Gọi góc giữa SB và mặt phẳng (SAD) là $60^\circ$, ta cần dựng tam giác SAB và SAD, tính độ dài SA.
Xét tam giác SAB vuông tại A:
AB = 2a, SA ⊥ mặt đáy ⇒ tam giác SAB vuông tại A
⇒ Dựng tam giác vuông SA vuông góc AB
Góc giữa SB và mặt phẳng (SAD) là góc giữa SB và hình chiếu của SB lên (SAD)
Gọi H là hình chiếu vuông góc của S lên mặt phẳng (ABCD), tức H ≡ A
Gọi $\alpha$ là góc giữa SB và mặt phẳng (SAD)
Dựng hình chiếu của SB lên mặt phẳng (SAD), hình chiếu đó chính là đường thẳng từ B vuông góc với mặt phẳng (SAD), giao tại điểm nào đó trên (SAD), nhưng vì SA ⊥ (ABCD), nên SB không có thành phần nghiêng trong đáy — mà hướng nghiêng phụ thuộc vào SA.
Sử dụng hệ thức lượng trong tam giác vuông:
Trong tam giác SAB vuông tại A, có:
Vậy thể tích:
V =
a) SC ⊥ (AEF)
b) Thể tích khối chóp SABCD là 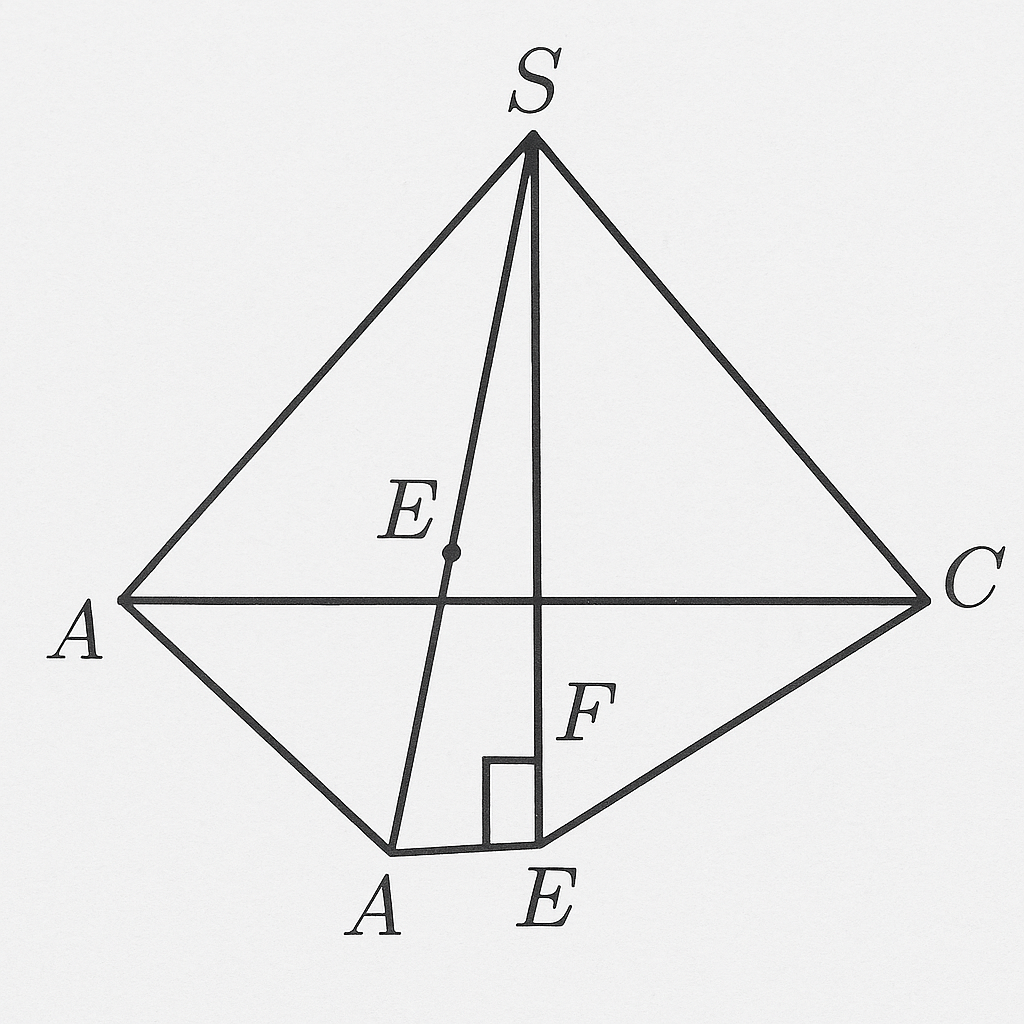
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
134838
Đã trả lời bởi chuyên gia
134838 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
75920
Đã trả lời bởi chuyên gia
75920 -
 Đã trả lời bởi chuyên gia
71641
Đã trả lời bởi chuyên gia
71641 -
 Đã trả lời bởi chuyên gia
47575
Đã trả lời bởi chuyên gia
47575


