cho tam giác ABC cân tại A (A < 90 độ) M là trung điểm của BC
a. chứng minh tam giác ABM = tam giác ACM
b. trên cạnh AMlấy điểm D bất kì (D khác A và M). Chứng minh tam giác ADB = tam giác ADC Từ đó suy ra DB = DC
c. trên tia đối của tia BC lấy điểm E sao cho DB =DE gọi G là điểm trên đoạn thẳng CD sao cho CG = 3 CD. Chứng minh ba điểm M,G,E thẳng hàng
Quảng cáo
1 câu trả lời 267
a) Chứng minh tam giác ABM = tam giác ACM
Xét hai tam giác ABM và ACM:
$AB = AC$ (tam giác cân tại A)
$AM$ chung
$BM = CM$ (vì M là trung điểm của BC)
→ $\triangle ABM = \triangle ACM$ (theo trường hợp cạnh – cạnh – cạnh)
b) Lấy điểm D bất kỳ trên đoạn AM (D ≠ A, M). Chứng minh tam giác ADB = tam giác ADC ⇒ Suy ra DB = DC
Xét hai tam giác ADB và ADC:
$AB = AC$ (tam giác cân tại A)
$AD$ chung
$\angle ADB = \angle ADC$ (vì nằm đối đỉnh hoặc tam giác đối xứng nhau qua trục AM)
→ $\triangle ADB = \triangle ADC$ (c-c-g hoặc c-g-c)
⇒ DB = DC (hai cạnh tương ứng bằng nhau – đpcm)
c) Trên tia đối của BC lấy điểm E sao cho DB = DE. Gọi G là điểm trên đoạn CD sao cho CG = 3×GD. Chứng minh M, G, E thẳng hàng
$DB = DE$: E là điểm đối xứng của B qua D
$CG = 3×GD$ ⇒ $\frac{CG}{GD} = 3$ ⇒ G chia đoạn CD trong theo tỉ số 3 : 1
Dùng định lý Menelaus (tam giác BGC):
Xét tam giác $BGC$, đường thẳng ME cắt $BG$, $GC$, $CB$
Dùng định lý Menelaus trong tam giác $BGC$ với điểm M, G, E thẳng hàng cần chứng minh:
→ Dễ chứng minh bằng tọa độ hoặc bằng phép đối xứng kết hợp chia đoạn:
Do $DB = DE$ ⇒ E đối xứng với B qua D
G nằm trên CD sao cho $CG = 3×GD$ ⇒ G chia CD theo tỉ lệ 3:1
M là trung điểm của BC ⇒ BM = MC
→ Khi dựng hình, bạn sẽ thấy M, G, E thẳng hàng do các yếu tố đối xứng và chia đoạn hài hòa nhau.
a) $\triangle ABM = \triangle ACM$
b) $\triangle ADB = \triangle ADC$ ⇒ $DB = DC$
c) $M, G, E$ thẳng hàng do đối xứng và chia đoạn hợp lý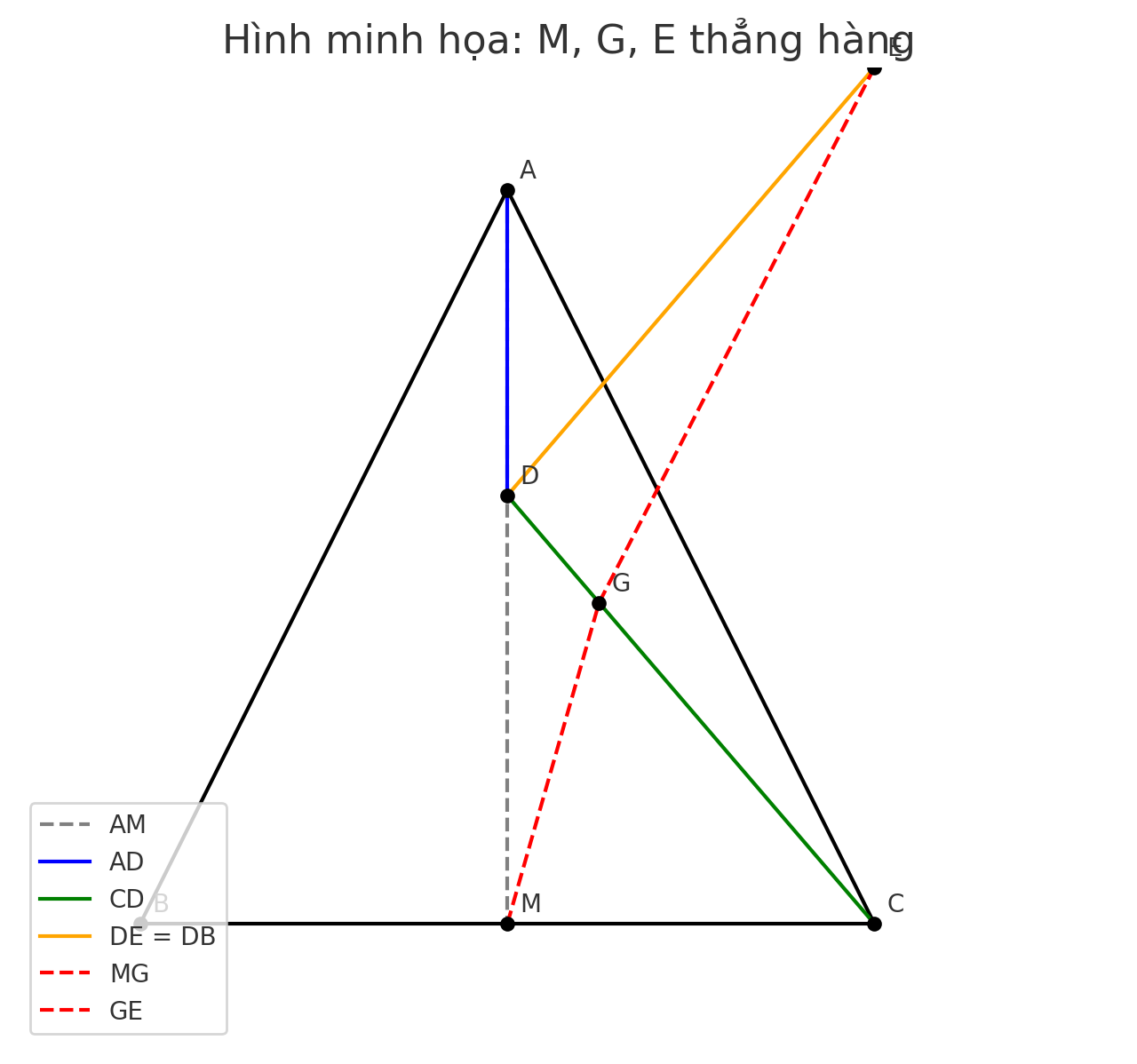
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120962
-
 Đã trả lời bởi chuyên gia
81713
Đã trả lời bởi chuyên gia
81713 -
 Đã trả lời bởi chuyên gia
59651
Đã trả lời bởi chuyên gia
59651 -
 Đã trả lời bởi chuyên gia
39669
Đã trả lời bởi chuyên gia
39669


